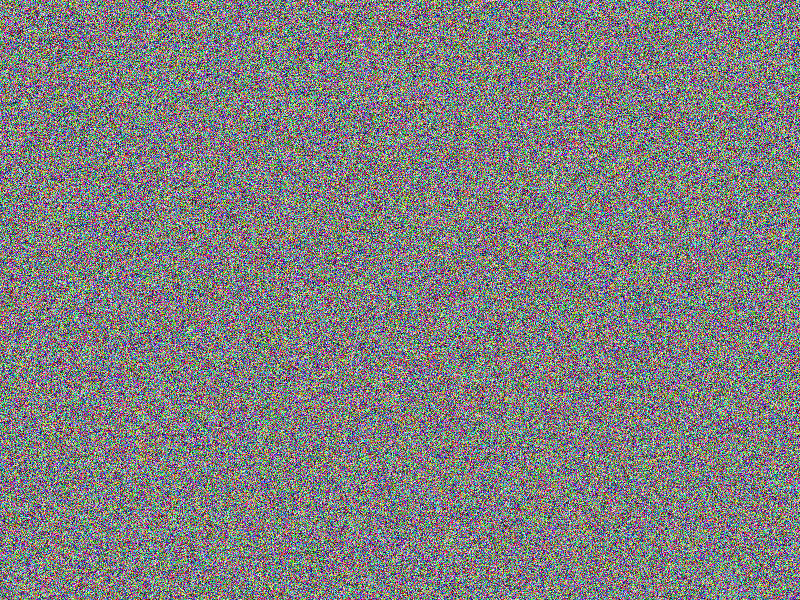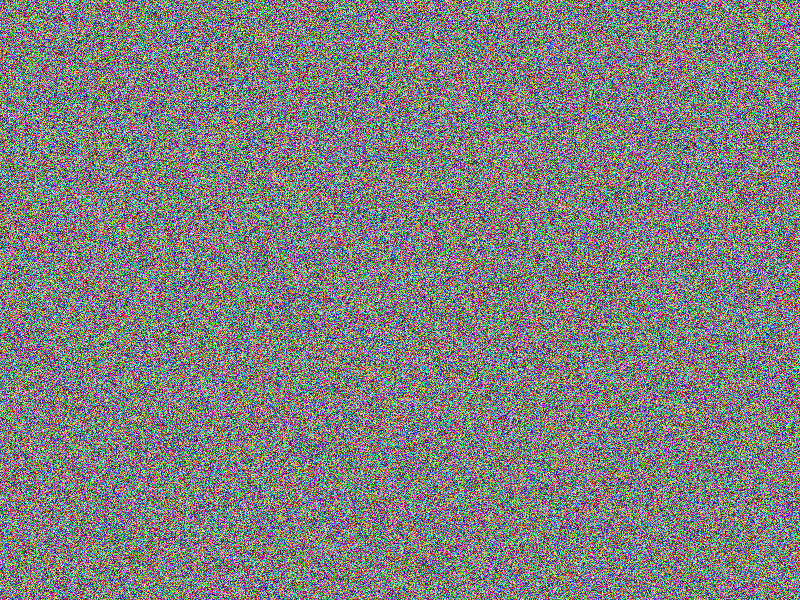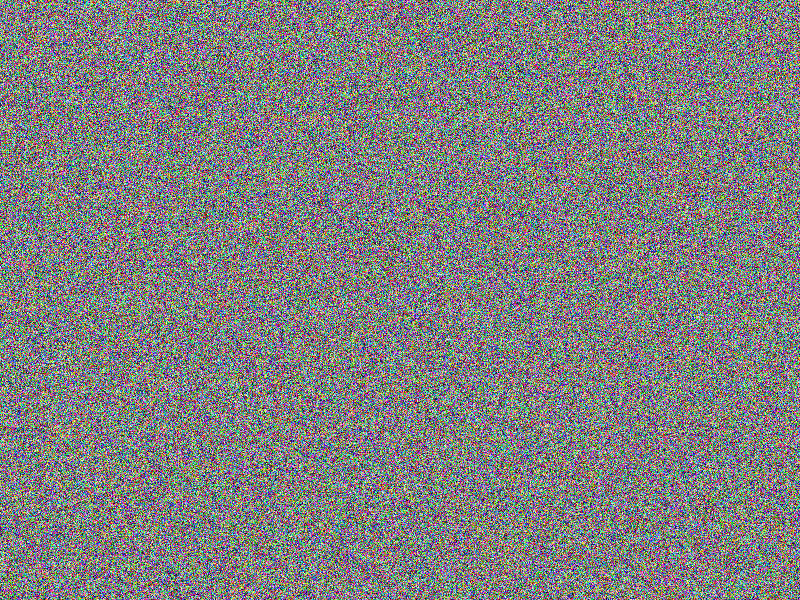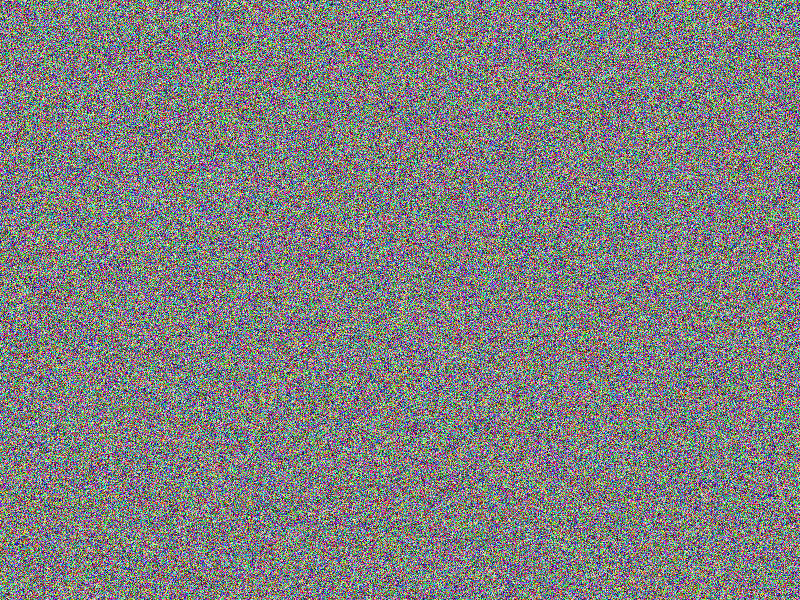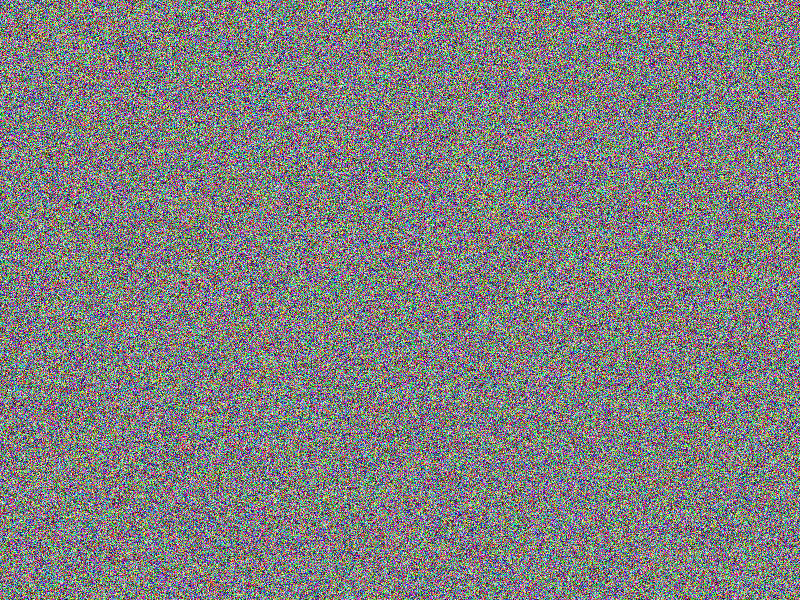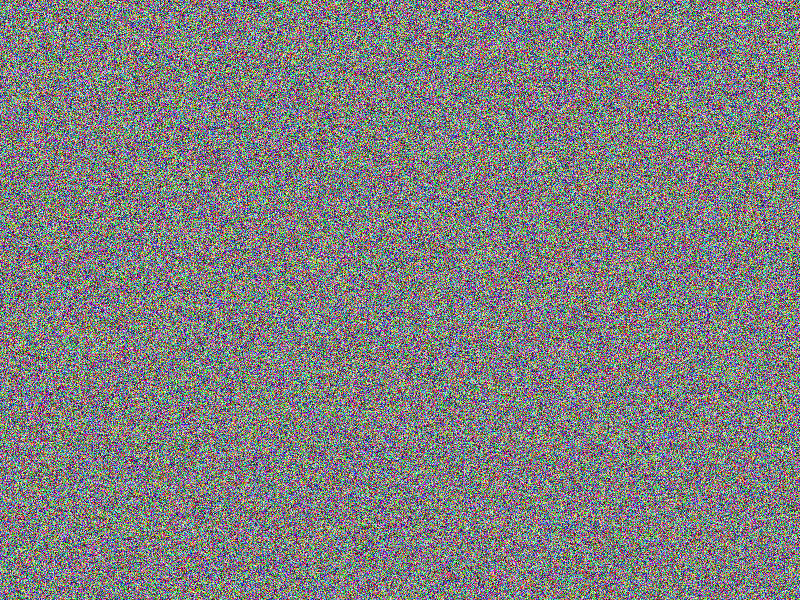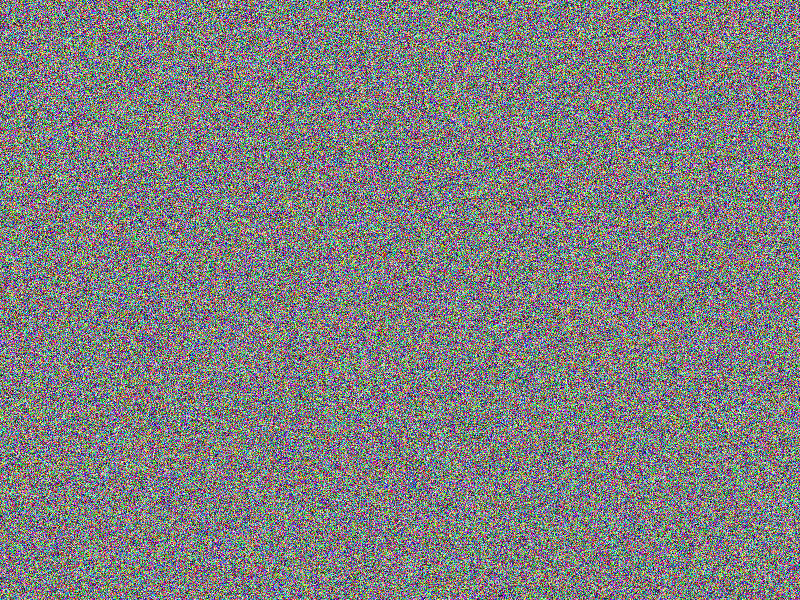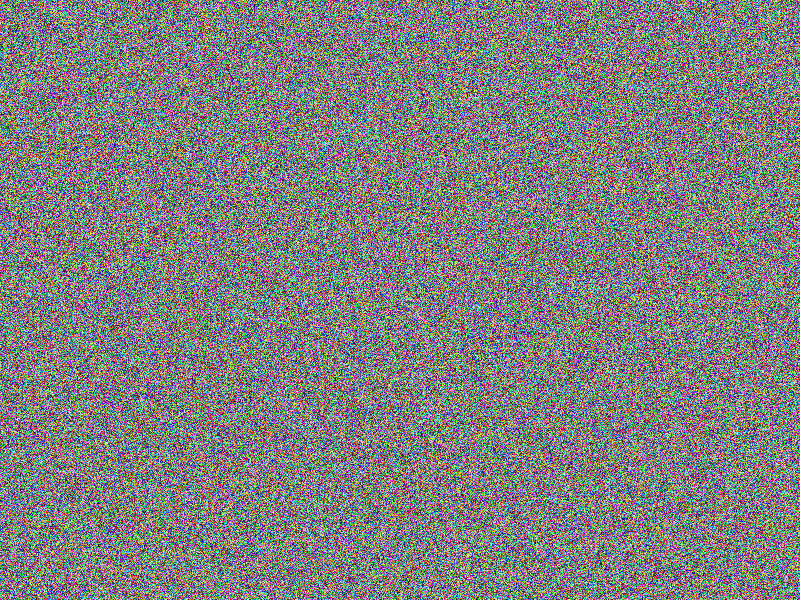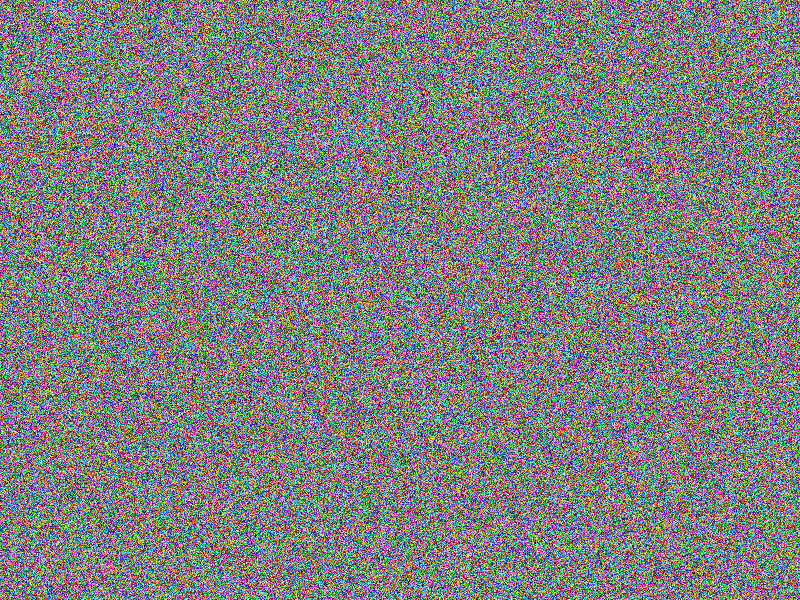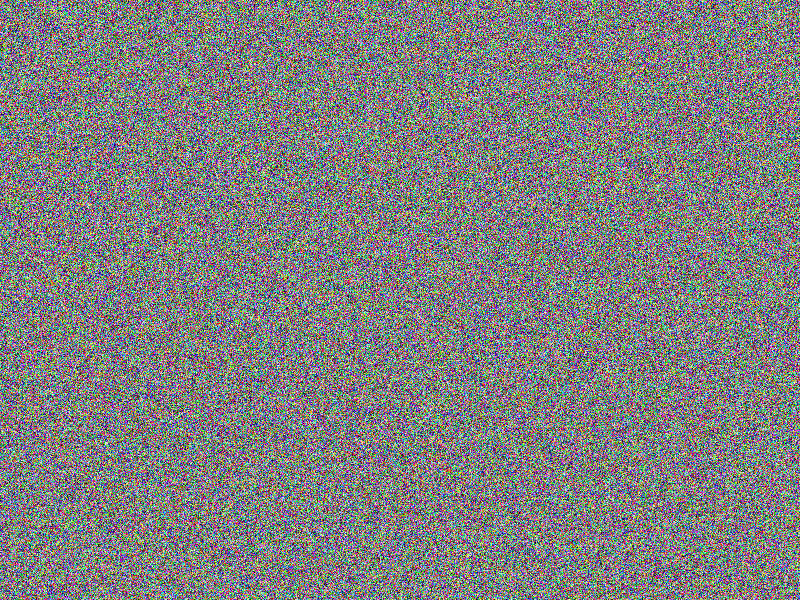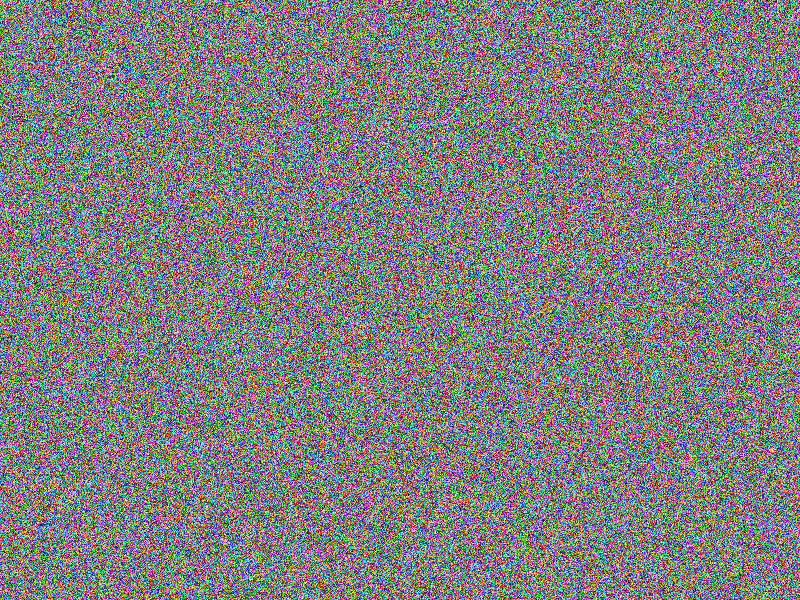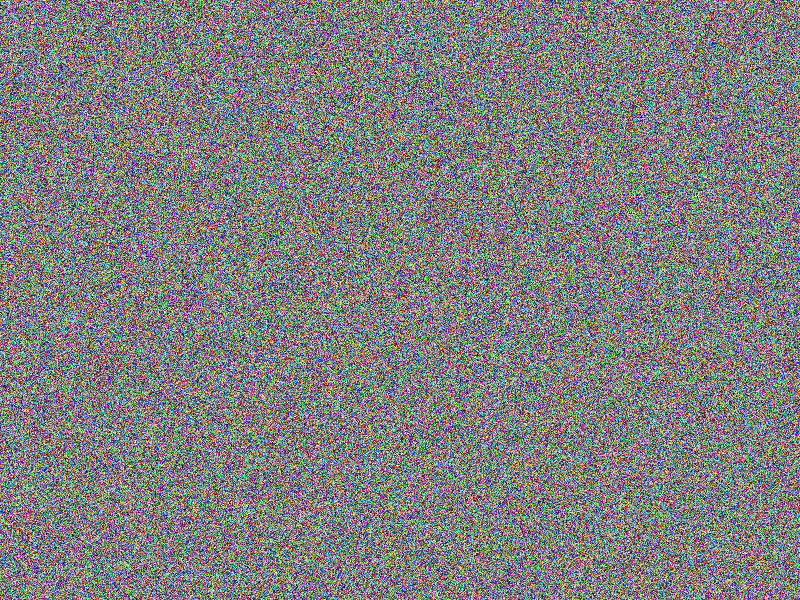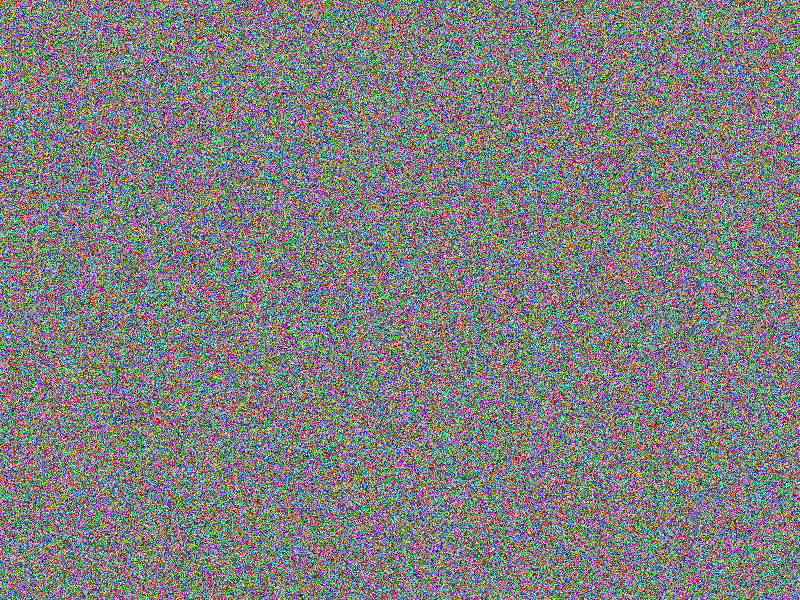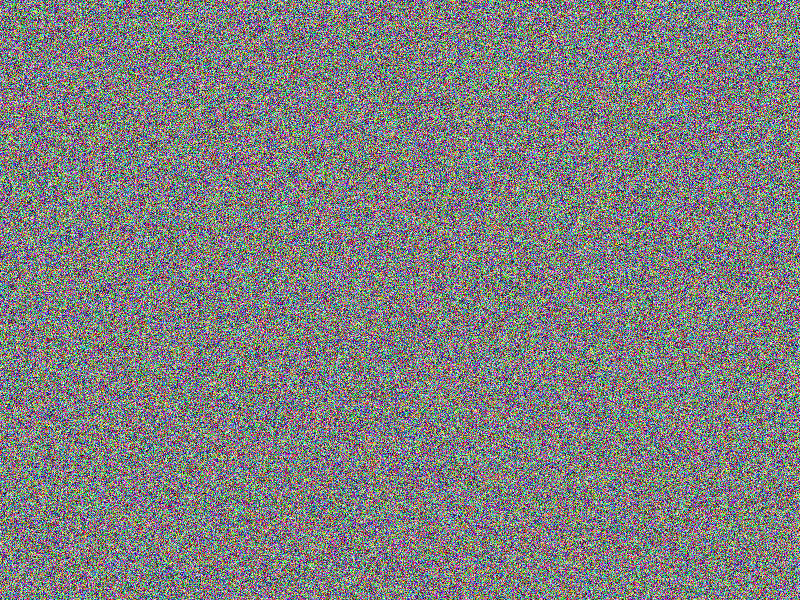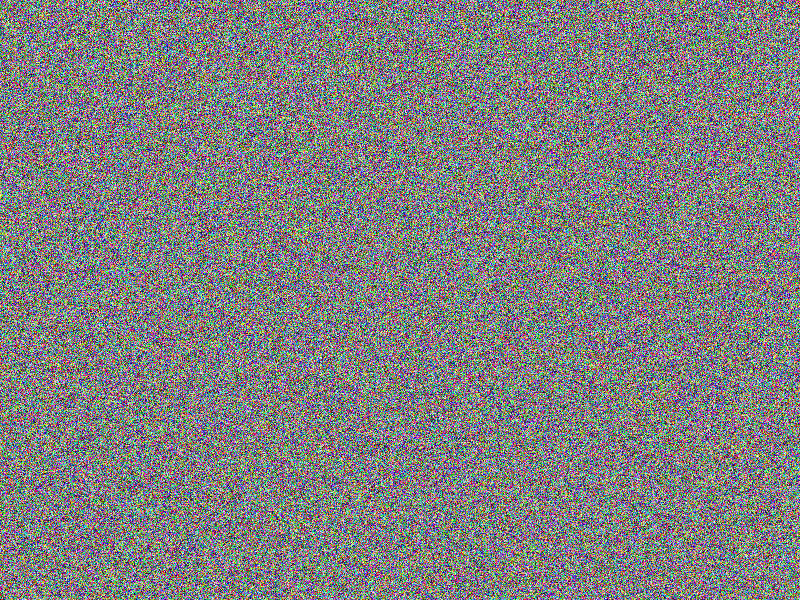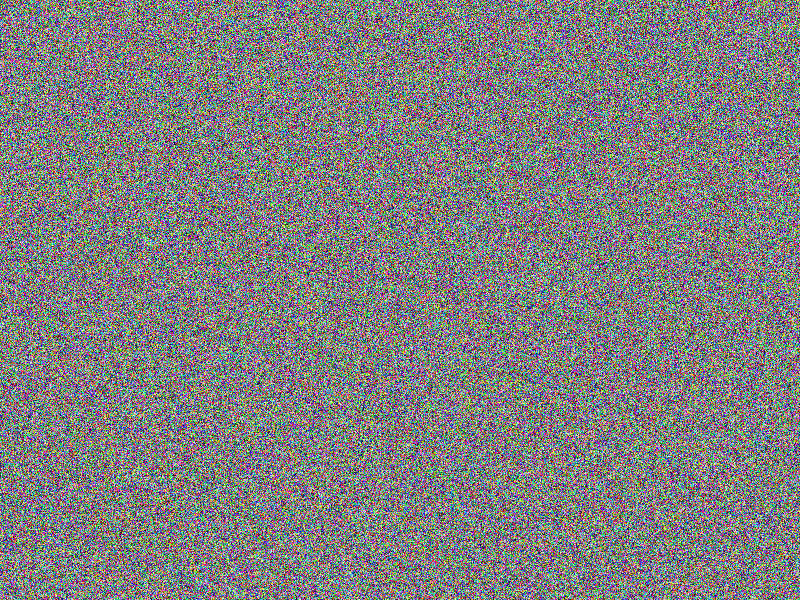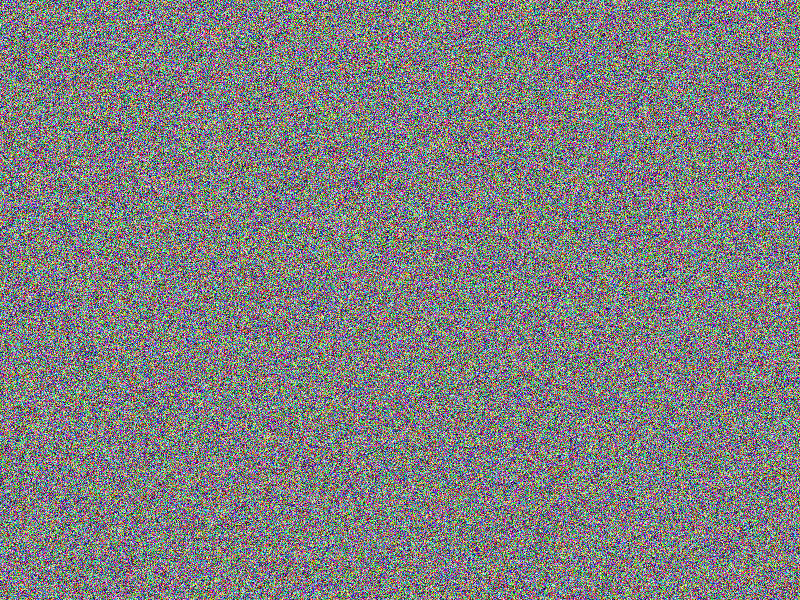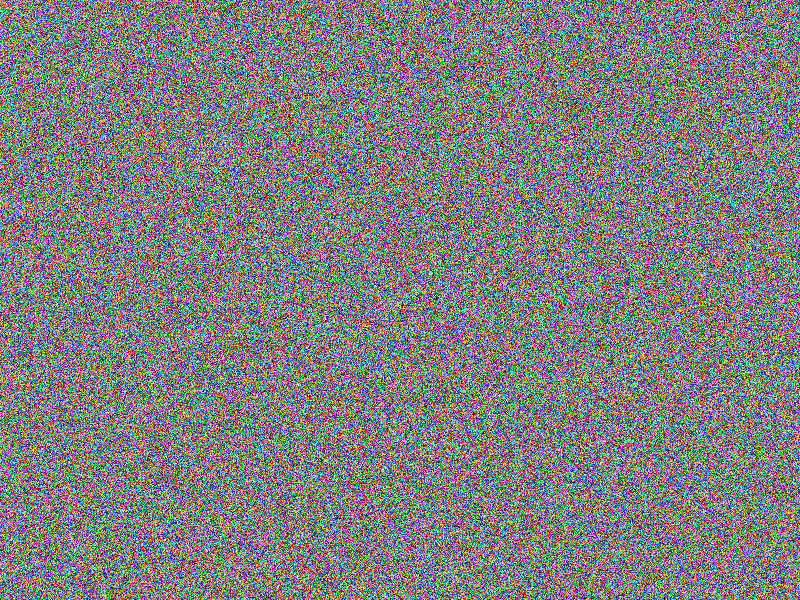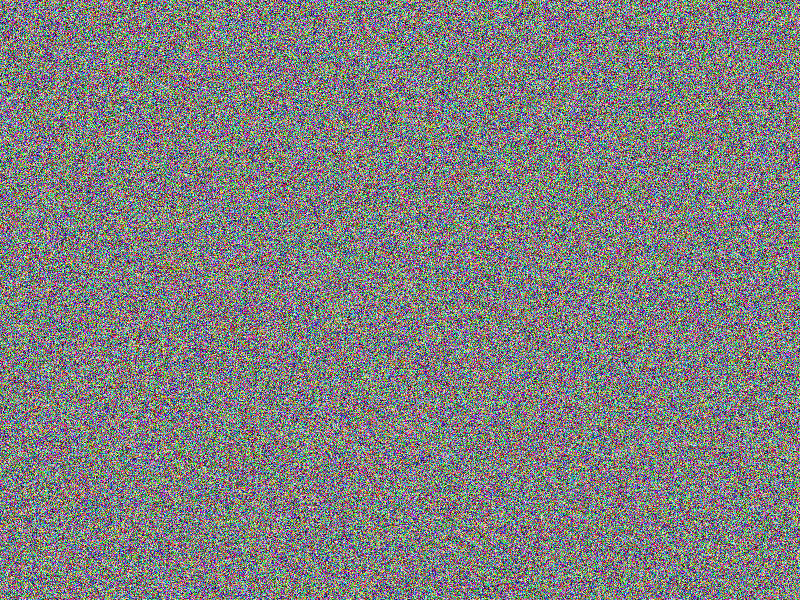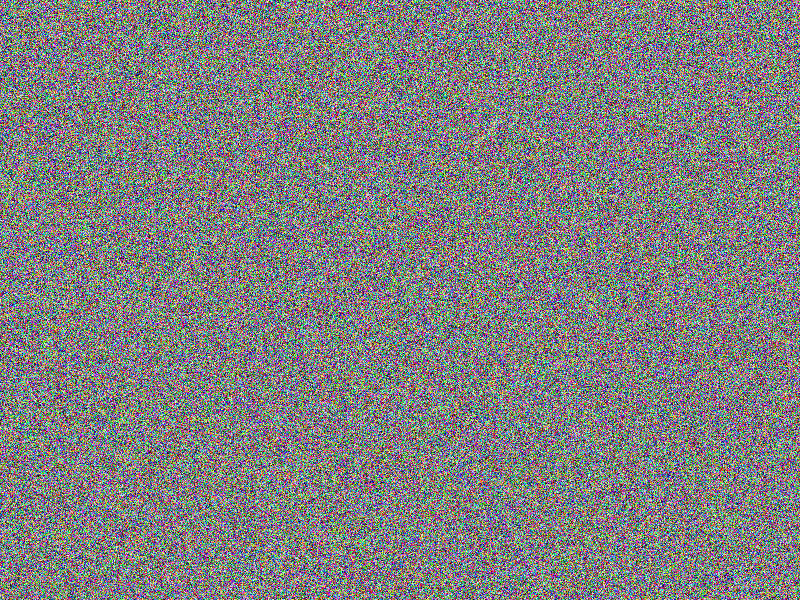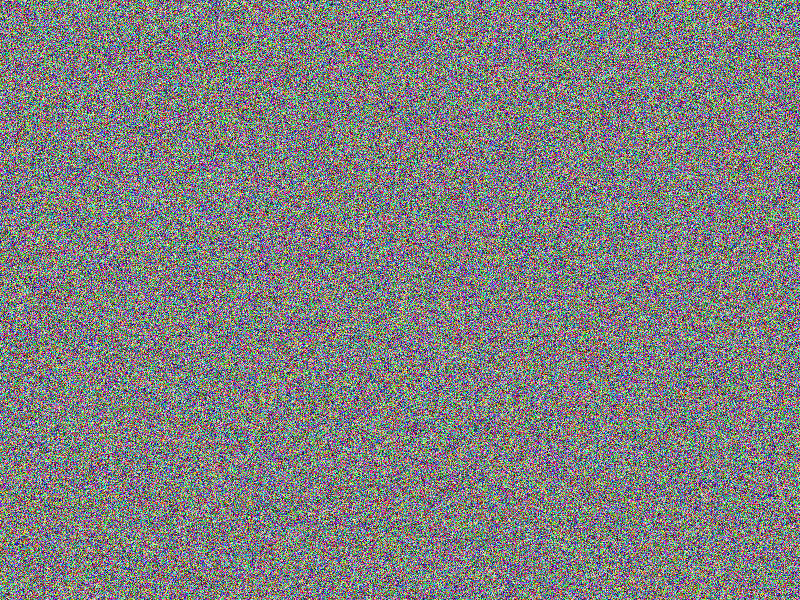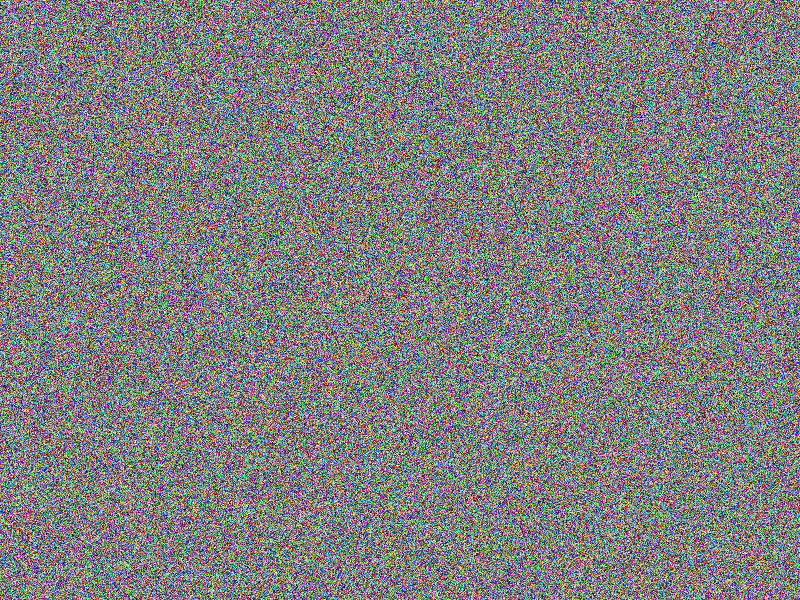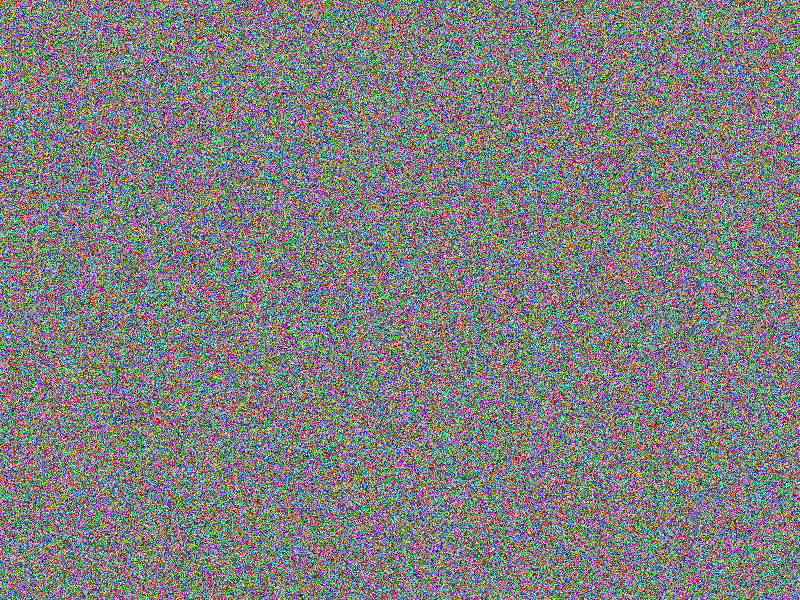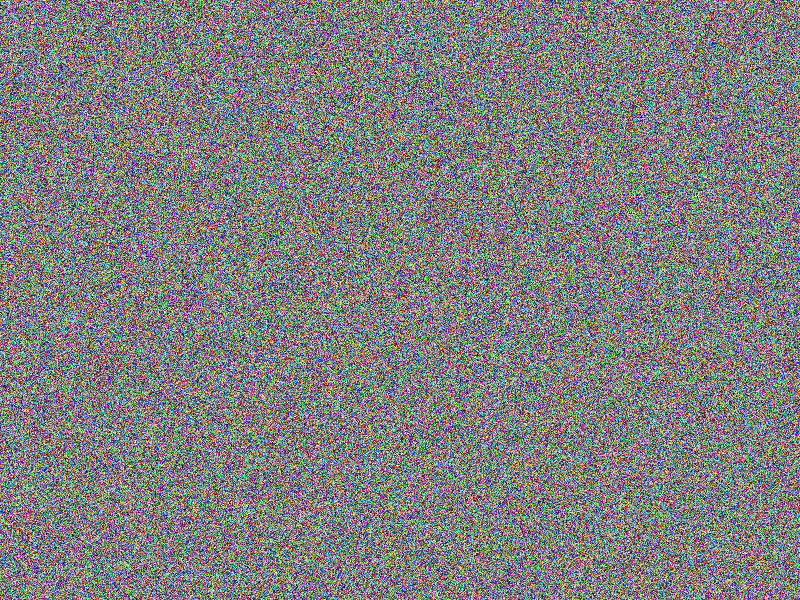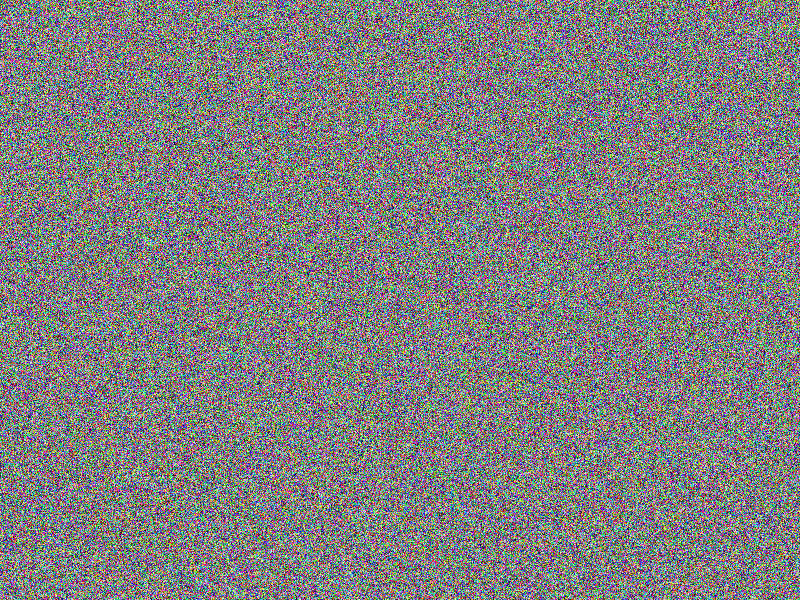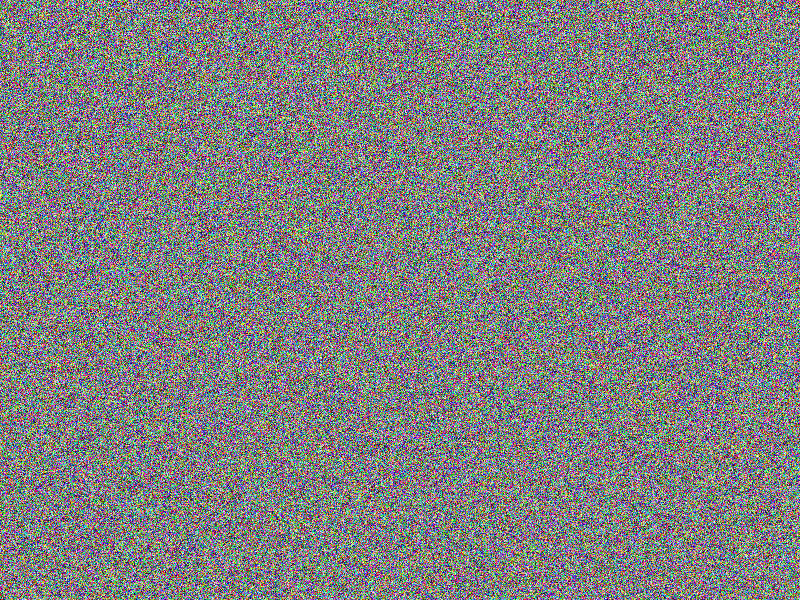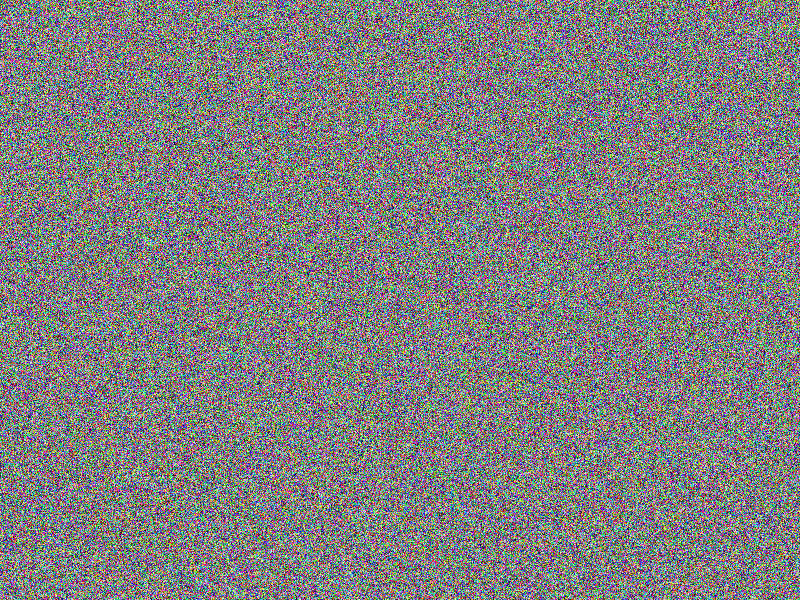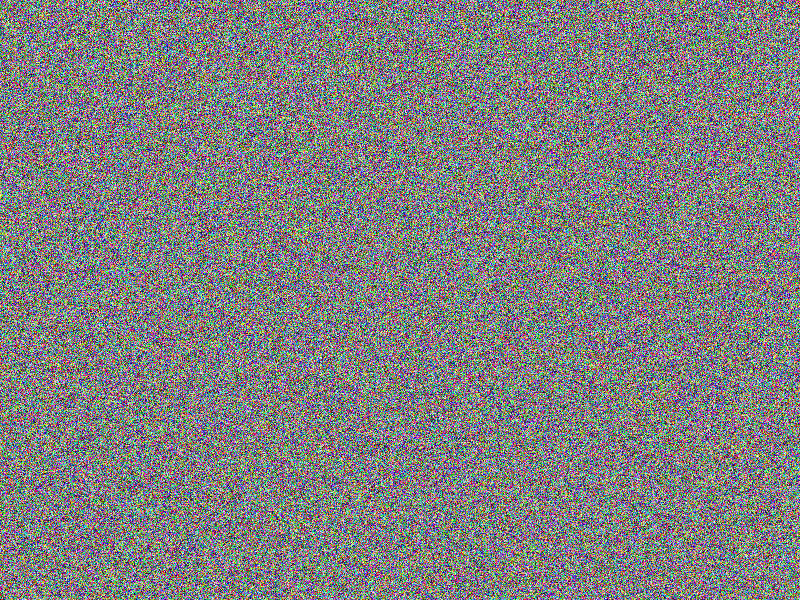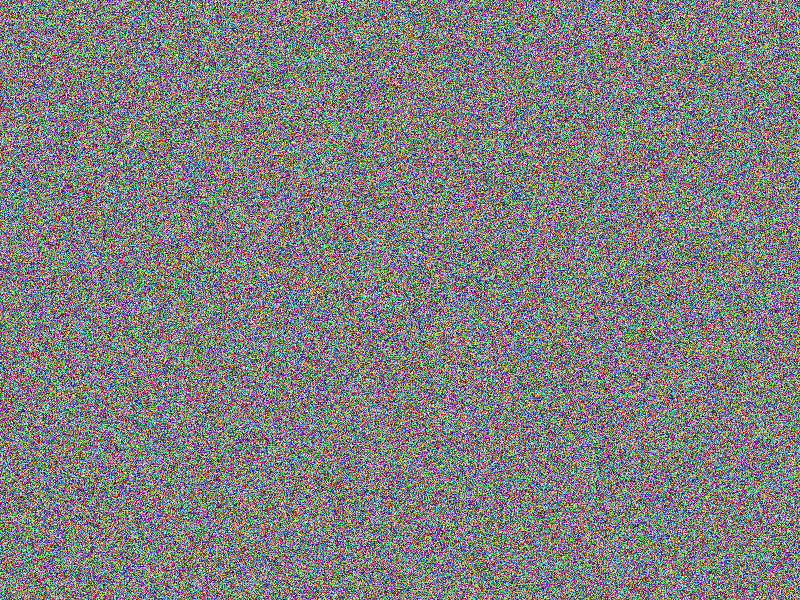Chaos-based encryption - revisited!

Chaos-based encryption - revisited!

Siegfried Steiner
Siegfried Steiner
17 min read

Categories

Tags

In the blog post Chaos-based encryption I introduced a chaotic cryptology algorithm1 using a Poincaré successor ordinal function. In this article I want to present you a command line suite providing this very Chaos-based encryption functionality alongside some extensions as well as comparison to the AES algorithm.

This chaos-based cryptography suite is intended for educational purposes only: As I am not a mathematician, I neither can guarantee the algorithm nor the program code implementing the algorithm to be water proof2 or free of bugs! Any usage is intended for educational purposes only and any other usage is at your own risk.

The show case

To evaluate the Chaos-based encryption command line suite I prepared some sample images A, B, C and D being similar to each other but different in some obvious details (except the last image being a photograph). Having those similar but differing images we can analyze the images (after being encrypted with a given algorithm) by comparing them with each other (samples) to get an idea on the effectiveness of the according algorithm.

Given similar but differing images we can analyze the accordingly encrypted images by visual comparison to get an impression of the effectiveness of the according algorithm.

As I already mentioned I am not a mathematician, hence I need some way to estimate the randomness and effectiveness of this command line suite by digging neither too deep into cryptography mathematics nor into abstract algebra. For a start I therefore decided to do some (non comprehensive) visual analysis (samples).

The setup

Given images A, B, C and D, I use a toolchain to extract the raw pixel data of each image, encrypt the raw pixel data with a given algorithm and convert the result back (interpreted as raw pixel data) into an image of the same dimensions.

In fact I used the PNG file format though the file format actually does not play a role. I could have chosen any other file format (supporting the required lossless compression and color depth ) and the visual result would have been the same as the analysis focuses on the raw pixel data (using PICDAT) and not on the physical image file as a whole (with its file header, compression method and so on).

The toolchain for the various steps during analysis consist of these four tools (the first two being available in the downloads section of this site:

  • PICDAT: Extracts raw pixel data from an image and the other way round
  • CHAOS: Encrypts and decrypts data based on Chaos-based encryption
  • OPENSSL: Encrypts and decrypts data based (amongst others) on the AES algorithm
  • ENT: Pseudorandom number sequence test for calculating the entropy on a stream of bytes
  • COMPARE: Mathematically and visually annotate the difference between an image and its reconstruction

The tool PICDAT I dedicatedly developed to accomplish visually analysing of (amongst others) Chaos-based encryption. Please see the sources for the actual compare-.sh as well as validate-.sh scripts automating the visual analysis as described below! The DADUM tool is similar in that I have developed it for creating loads of data to test your algorithms (though it was not needed in this setup).

Overview

First of all, the raw image data of the sample images A, B, C and D is extracted using PICDAT3. Then the raw image data of each image is being encrypted with various flavors of the AES and the CHAOS algorithms respectively (see below), using openssl for the AES-* variants and CHAOS3 for the CHAOS-* variants.

  A B C D
Original Blank canvas Black and white squares Squares with circle Old photograph
AES-256-ECB Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
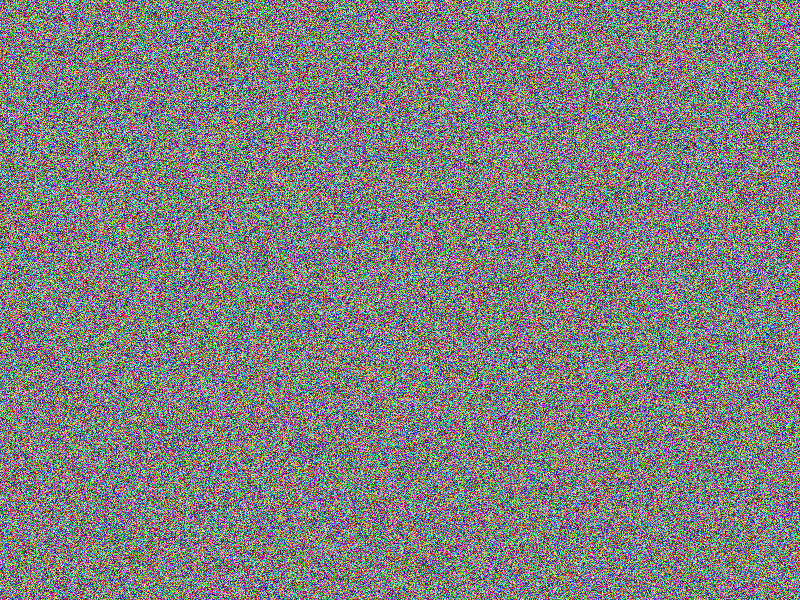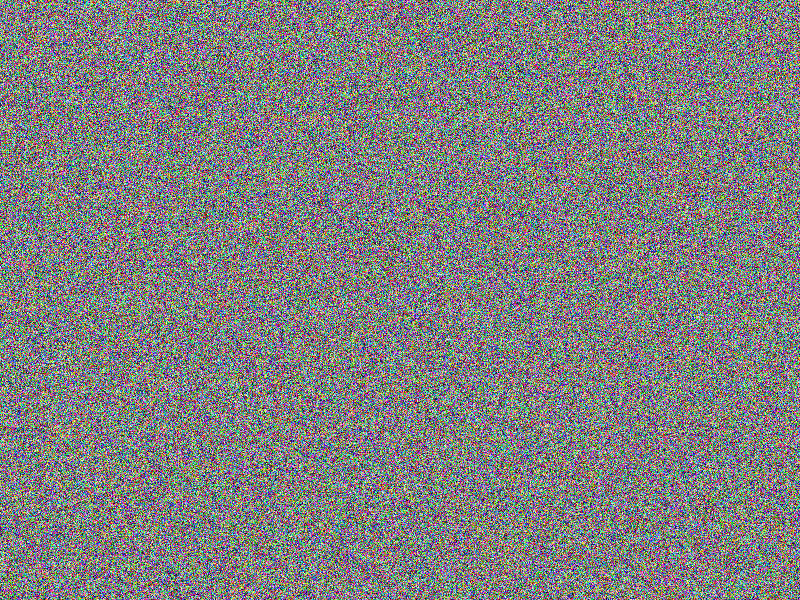AES-256-ECB-SALTED Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
AES-256-CBC Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
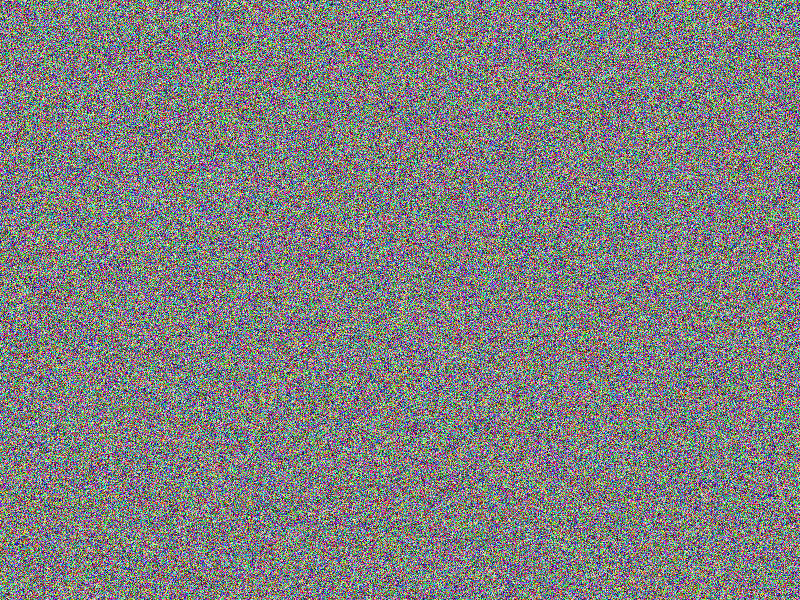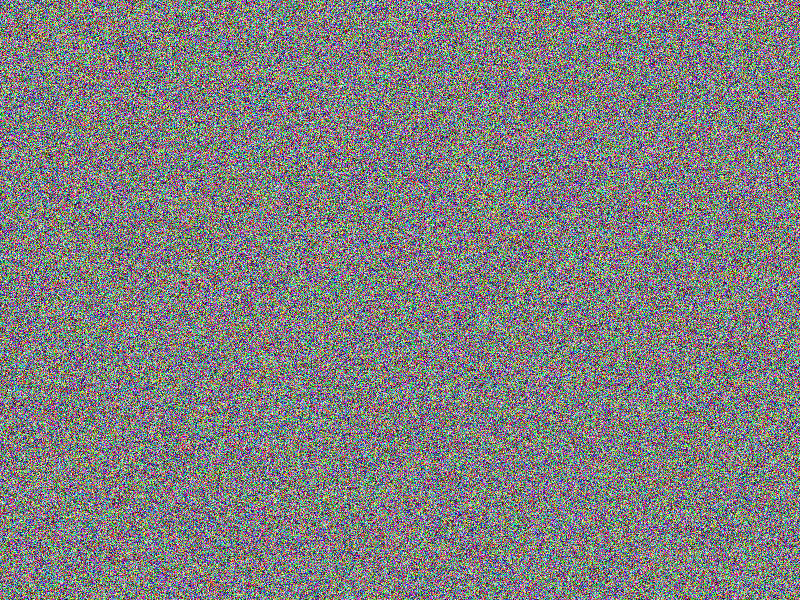AES-256-CBC-SALTED Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
CHAOS-NONE Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
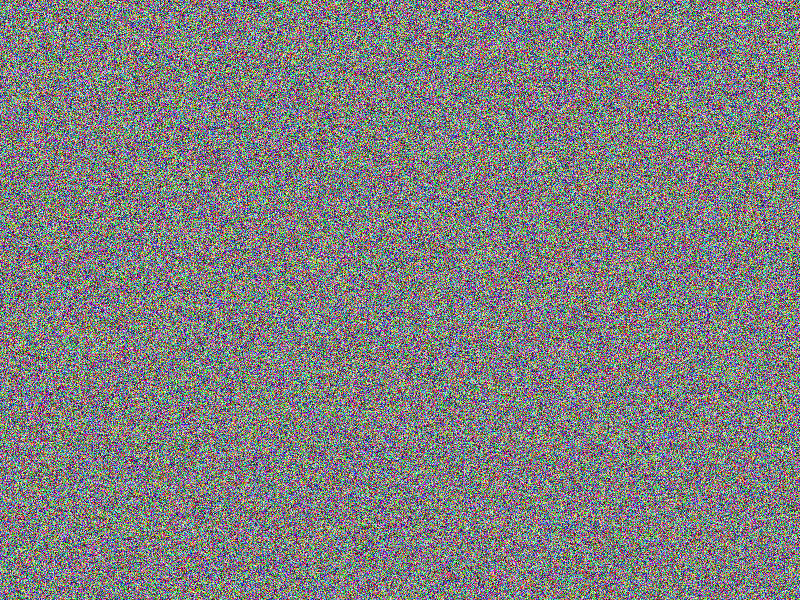CHAOS-XOR Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
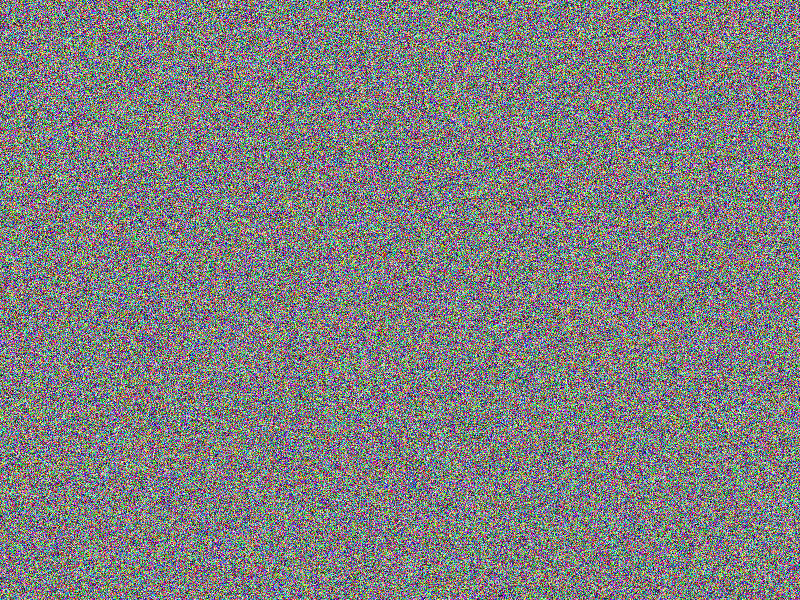CHAOS-MUTATE Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
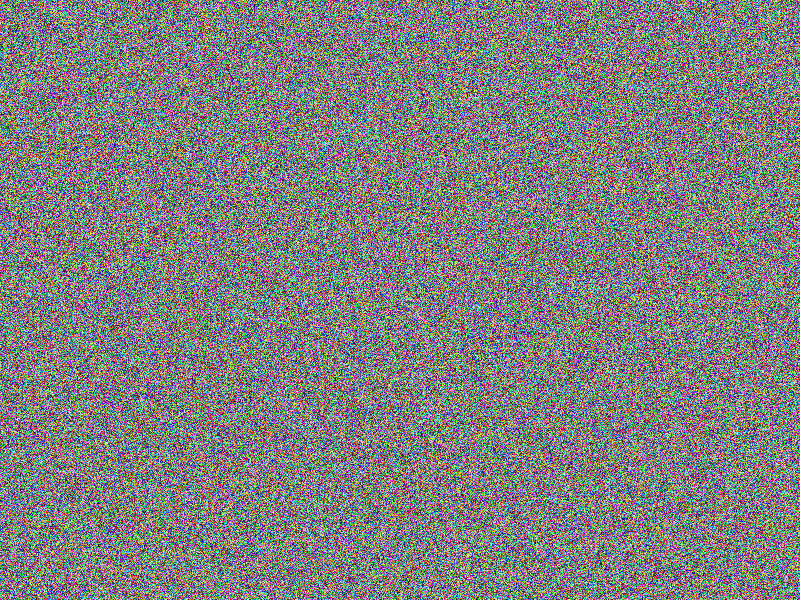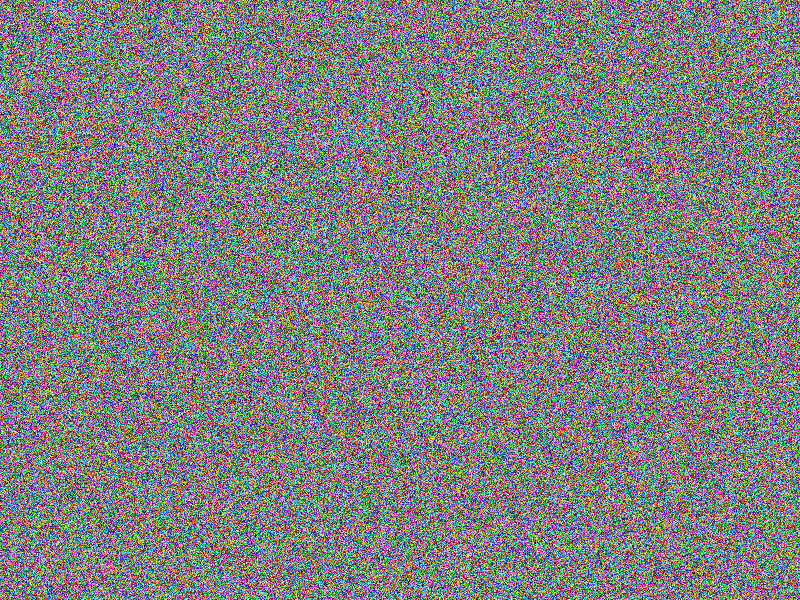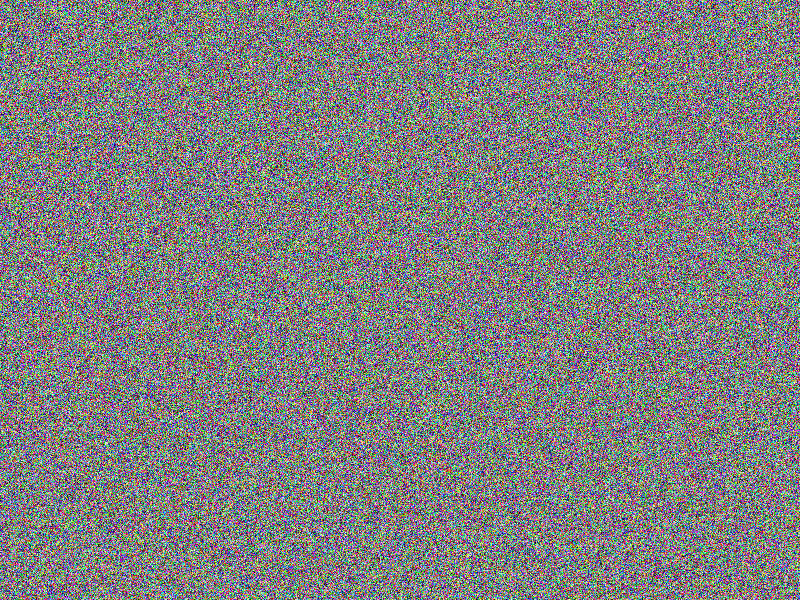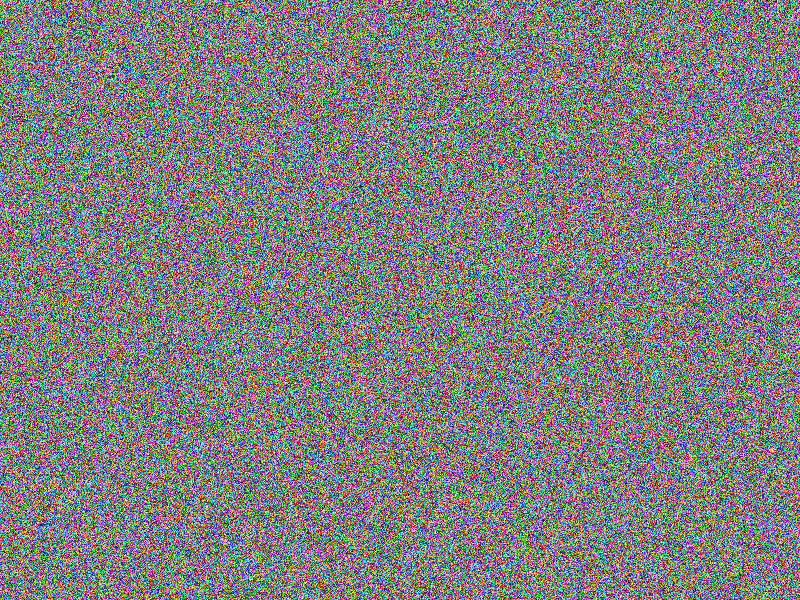CHAOS-PREFIX32 Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
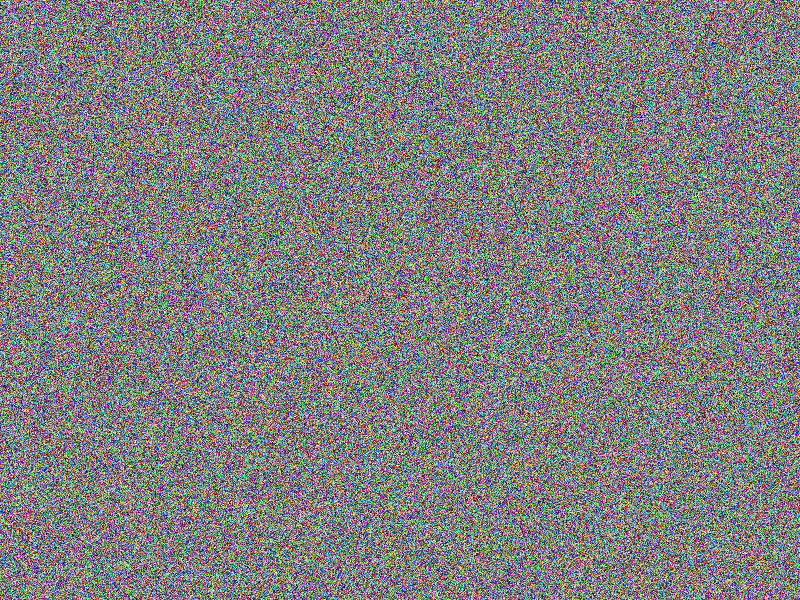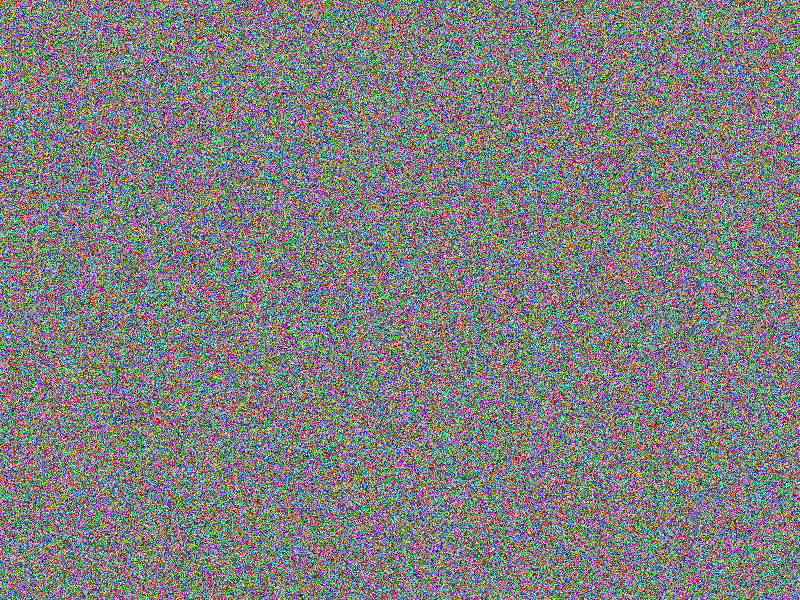CHAOS-M.-XOR Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
CHAOS-M.-P.32 Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
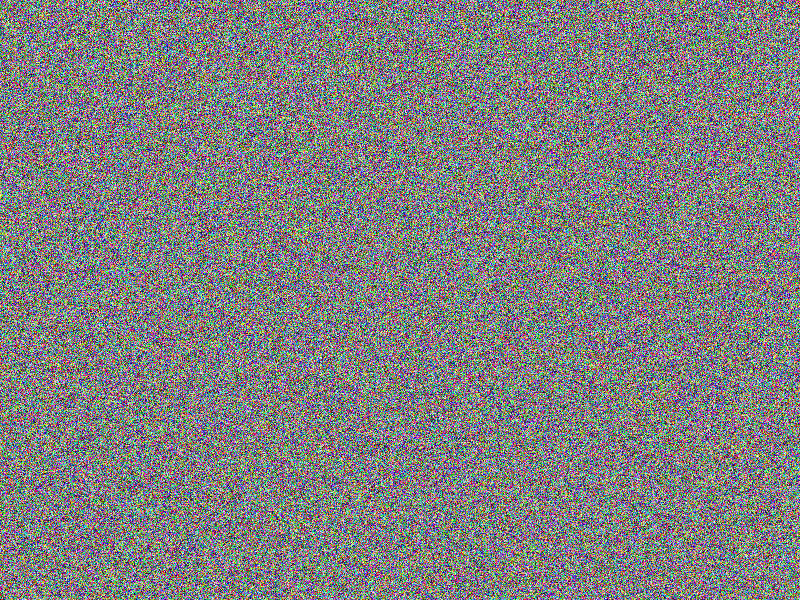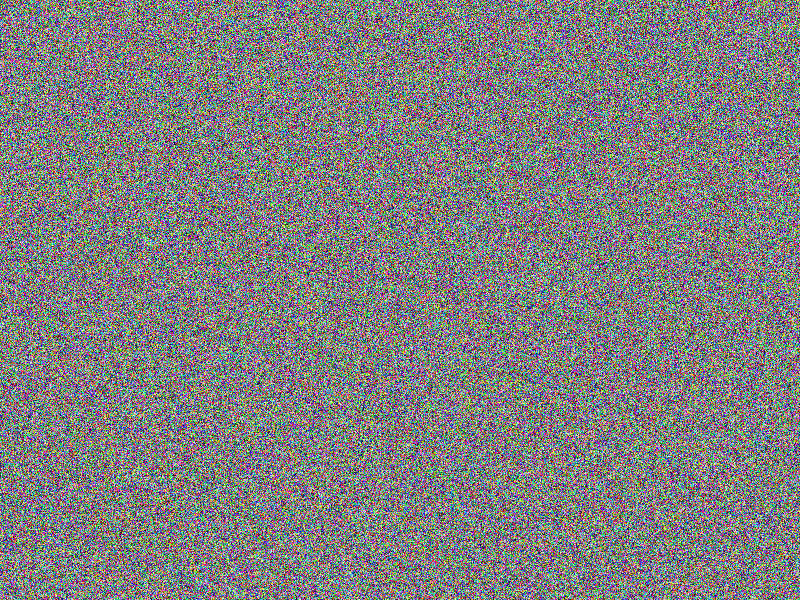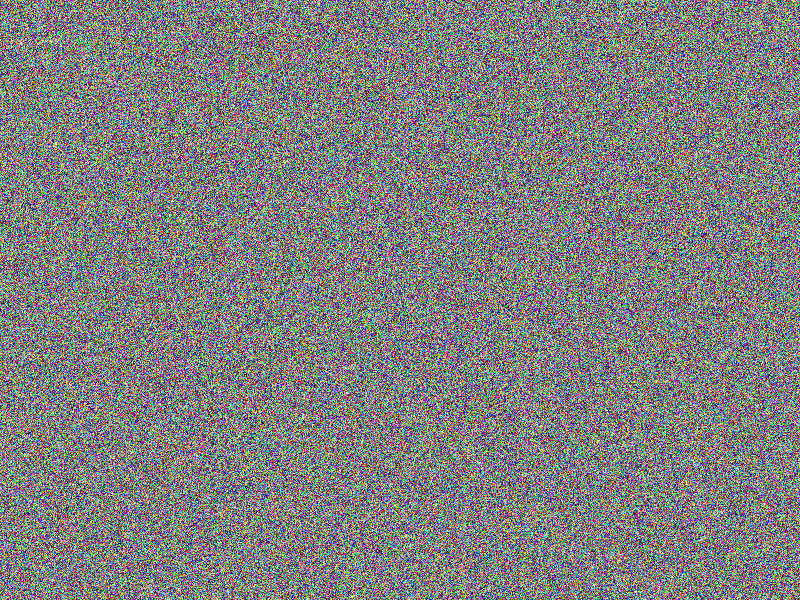CHAOS-M.-XOR-P.32 Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
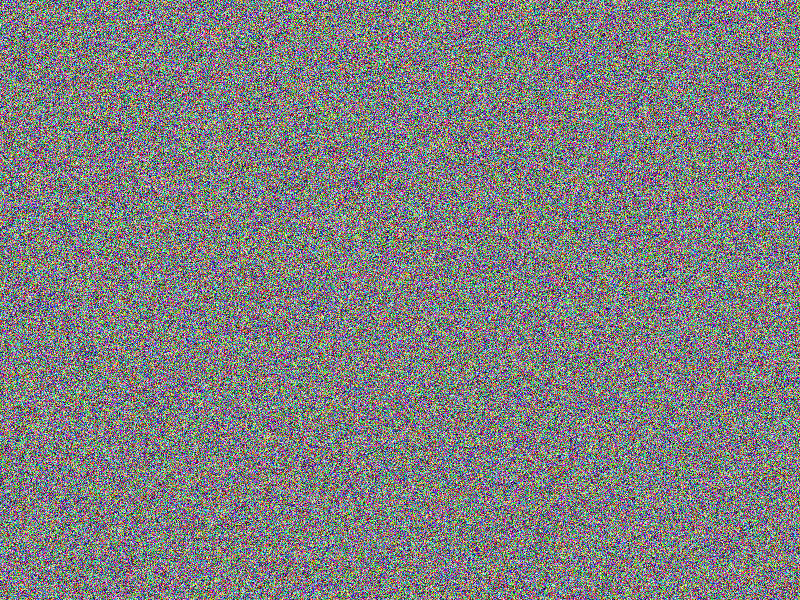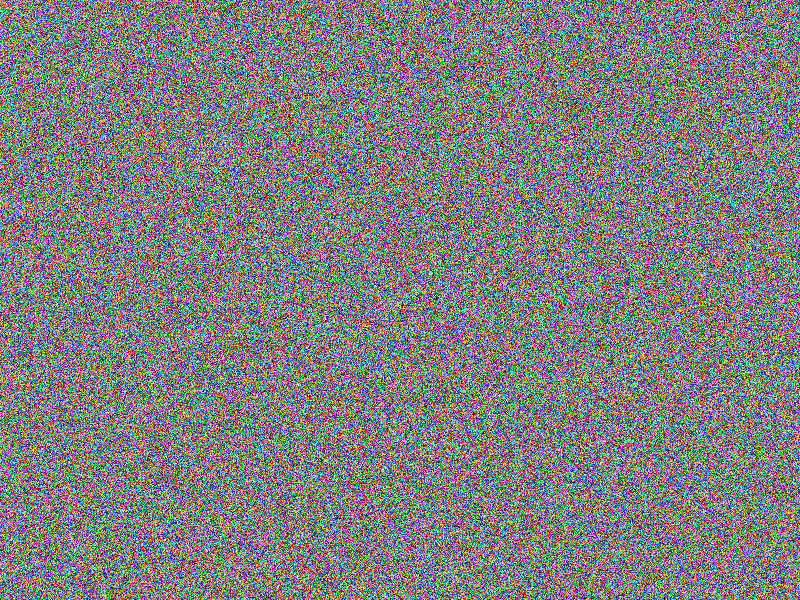CHAOS-SALTED Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph
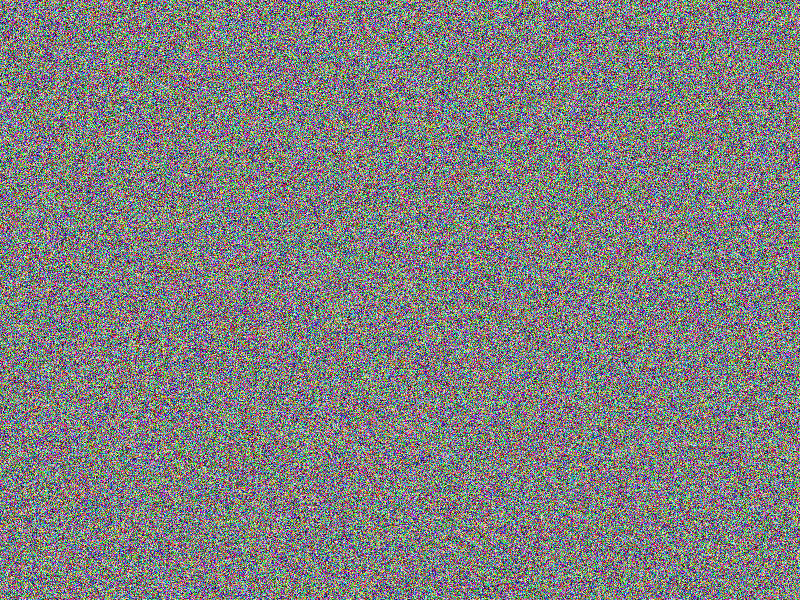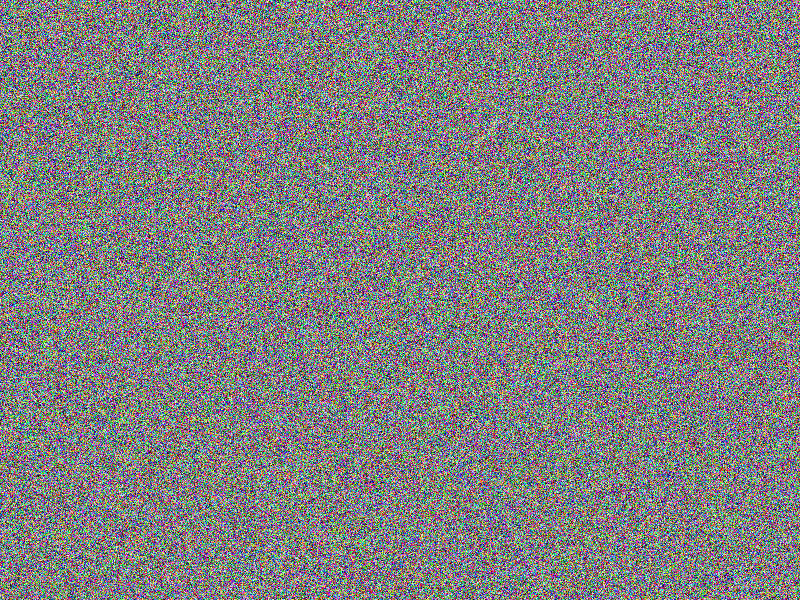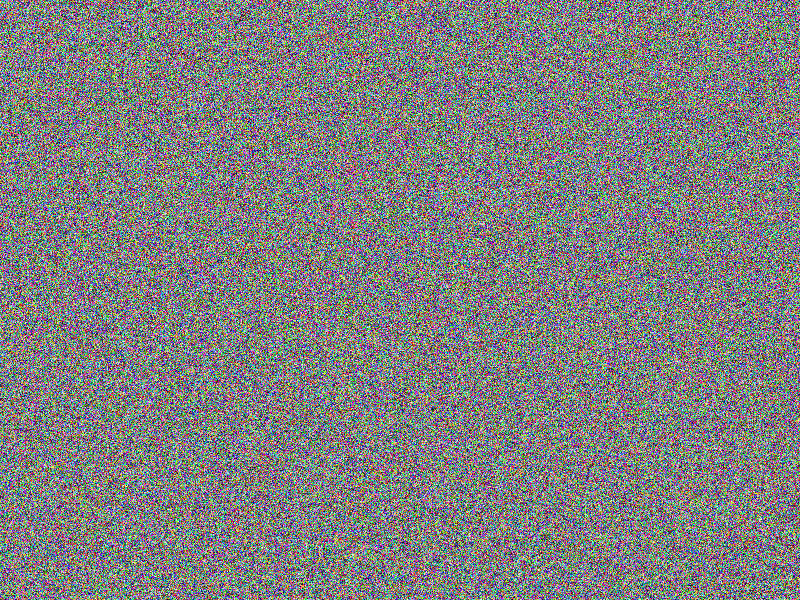CHAOS-CERT Encrypted blank canvas Encrypted black and white squares Encrypted squares with circle Encrypted old photograph

Taking a look at image A (raw) data’s metrics with no encryption applied we get the following values:

  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Entropy bits/byte (8 = best): 0
  • Arithmetic mean (127.5 = random): 255
  • Serial correlation (none = 0.0): -100000
  • Max compression (0% = none) = 100%

As the image is a blank (white) image, its raw data consists of an accordingly large number of bytes with values 255 (0xFF) as a white pixel is represented by a sequence of bytes with (again) a value of 255 (0xFF). Hence we get an arithmetic mean of 255 (0xFF).

For a good cryptographic algorithm I would expect the entropy (bits per byte) to be very near to 8, the arithmetic mean to be very near to 127.5, the serial correlation to be very near to 0.0 and the max compression to be very near to 0%.

Observations

The below “Samples” section illustrates the various algorithms’ variants by comparing two very similar encrypted images A, B and C with each other: The bottom right images each are the result of a COMPARE operation between the according (encrypted) image directly to the left and the according (encrypted) image directly above that resulting image: Same areas between both images are colored gray ■ in the resulting image, differing areas are colored red ■, so that the difference between two images may give a hint on the content of the images (a fully red area as a result of comparison would be aspirable).

AES

At a first sight, AES-256 (ECB) encryption still provides a quite good impression on what has been encrypted, even AES-256 (ECB-SALTED) salting4 does not ease the situation. This is a known “feature” of of the electronic codebook (ECB) mode used here. Furthermore, the comparison of the AES-256 (ECB) encrypted images allows conclusions to be drawn about the original images’ content (see the according bottom right images). At least salting4 with AES-256 (ECB-SALTED) makes comparing two very similar encrypted images challenging (notice the according bottom right image being fully red, indicating no equal areas). Having a glance at the encrypted images we are better off with AES-256 (CBC), providing no immediate hint on the content. Still, comparing two very similar images encrypted using AES-256 (CBC) reveal similar areas till the position where the images actually differ the fist time (notice the according bottom right image’s gray areas, indicating equal areas). Using AES-256 (CBC-SALTED) looks perfect in that the comparison reveals no equal areas (notice the according bottom right image being fully red, indicating no equal areas) and the encrypted images look fully random.

CHAOS

As of the CHAOS comparisons we can see the evolution of the CHAOS command: Vanilla plain CHAOS (NONE) encryption does not reveal immediate correlation to the content of the original images (there seems already to be a quite good randomness), although the comparison of the CHAOS (NONE) encrypted images gives a first impression of the original images’ content (see the according bottom right images). To soothe this situation, CHAOS (XOR), CHAOS (PREFIX32) as well as CHAOS (MUTATE) flavors adding some obfuscation were introduced without a convincing result. At least the combination of all three CHAOS (MUTATE-XOR-PREFIX32) variants seems to do the trick, any other combination “did not work out”. To not rely on this combination of obfuscations, as this could have been pure coincidence (regarding the chosen images), a salting CHAOS (SALTED) flavor has been implemented. This reliably prevents easily getting an idea of the content by simply comparing the encrypted images. For scaling purposes, the CHAOS (CERT) addition has been added, providing means to apply an arbitrary number of encryption passes using a certificate of detailed instructions for each pass: Hence multiple passes with a mixture of obfuscation methods can be applied, including XOR, PREFIX, MUTATE or SLATED obfuscations, alongside individual encryption keys, elongating the resulting “key” and hardening against brute force attacks.

Critical reflection

In their publication on Chaos-Based Cryptography: End of the Road?, Iercan, D., Dranga, O., Dragan, F. and Banias, O identify a weakness of chaos-based encryption being the “dynamic degradation of digital chaotic systems”:

“… Chaos-based cryptography emerged in the early 1990s as an innovative application of nonlinear dynamics in the chaotic regime. Even if in theory chaotic dynamics was thought to evolve into a new revolution in cryptography, in real-life an efficient and reliable chaos-based cryptosystem didn’t emerge. The main but not the only reason is the dynamic degradation of digital chaotic systems, a subject that became very popular in the last few years. This paper presents a new theoretical background related to this issue that proves the inefficiency of chaos-based encryption algorithms. Even more, in one of the two relevant case studies presented, another myth is demolished: the analog encryption base on synchronized chaos …” Chaos-Based Cryptography: End of the Road?

(I cannot tell whether this applies to Chaos-based encryption using a Poincaré successor ordinal function as described in this article, or not)

Samples

The below samples illustrate the various algorithms’ variants by comparing two very similar encrypted images A, B and C with each other: The bottom right images each are the result of a COMPARE operation between the according (encrypted) image directly to the left and the according (encrypted) image directly above that resulting image: Same areas between both images are colored gray ■ in the resulting image, differing areas are colored red ■, so that the difference between two images may give a hint on the content of the images (a fully red area as a result of comparison would be aspirable).

AES

AES-256 (ECB) encryption

The encryption still provides quite good impression on what has been encrypted. This is a known “feature” of of the electronic codebook (ECB) mode used here. Furthermore, the comparison of the encrypted images allows conclusions to be drawn about the original images’ content (see the according bottom right images).

Facts

  • Algorithm: AES-256-ECB
  • Key size: 256 bits (32 Bytes)
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 165
  • Entropy bits/byte (8 = best): 4.000186
  • Arithmetic mean (127.5 = random): 102.062991
  • Serial correlation (none = 0.0): -0.248134
  • Max compression (0% = none): 49%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

AES-256 (ECB-SALTED) encryption

Encryption still provides a quite good impression on what has been encrypted, although salting4 has been applied. This is a known “feature” of of the electronic codebook (ECB) mode used here. At least salting4 makes comparing two very similar encrypted images challenging (notice the according bottom right image being fully red, indicating no equal areas).

Facts

  • Algorithm: AES-256-ECB-SALTED4
  • Key size: 256 bits (32 Bytes)
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 165
  • Entropy bits/byte (8 = best): 4.000373
  • Arithmetic mean (127.5 = random): 90.938478
  • Serial correlation (none = 0.0): -0.065746
  • Max compression (0% = none): 49%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

AES-256 (CBC) encryption

Encryption does not provide an immediate hint on the content. Still, comparing two very similar images reveal similar areas till the position where the images actually differ the fist time (notice the according bottom right image’s gray areas, indicating equal areas).

Facts

  • Algorithm: AES-256-CBC
  • Key size: 256 bits (32 Bytes)
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 165
  • Entropy bits/byte (8 = best): 7.999896
  • Arithmetic mean (127.5 = random): 127.455223
  • Serial correlation (none = 0.0): -0.000401
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) 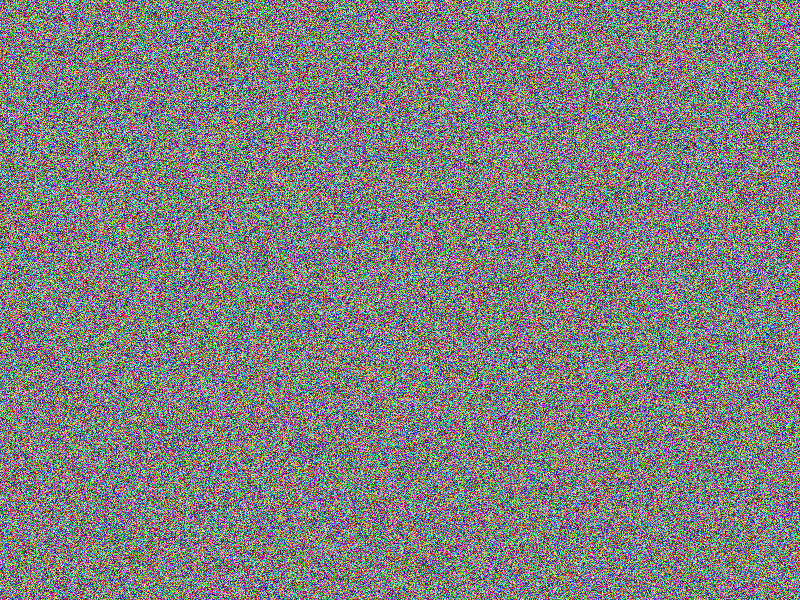Encrypted black and white squares
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
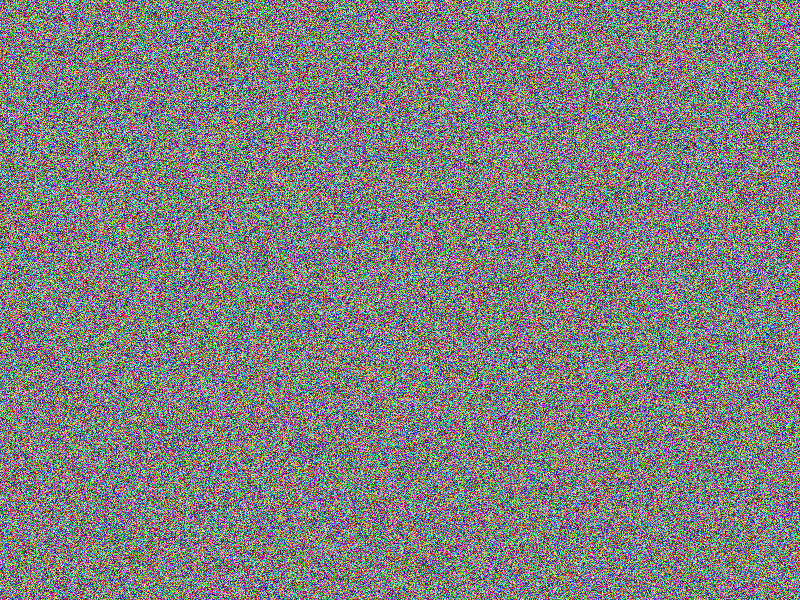B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

AES-256 (CBC-SALTED) encryption

Salted 4 encryption looks perfect in that the comparison reveals no equal areas (notice the according bottom right image being fully red, indicating no equal areas) and the encrypted images look fully random.

Facts

  • Algorithm: AES-256-CBC-SALTED4
  • Key size: 256 bits (32 Bytes)
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 165
  • Entropy bits/byte (8 = best): 7.999867
  • Arithmetic mean (127.5 = random): 127.536467
  • Serial correlation (none = 0.0): -0.000888
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
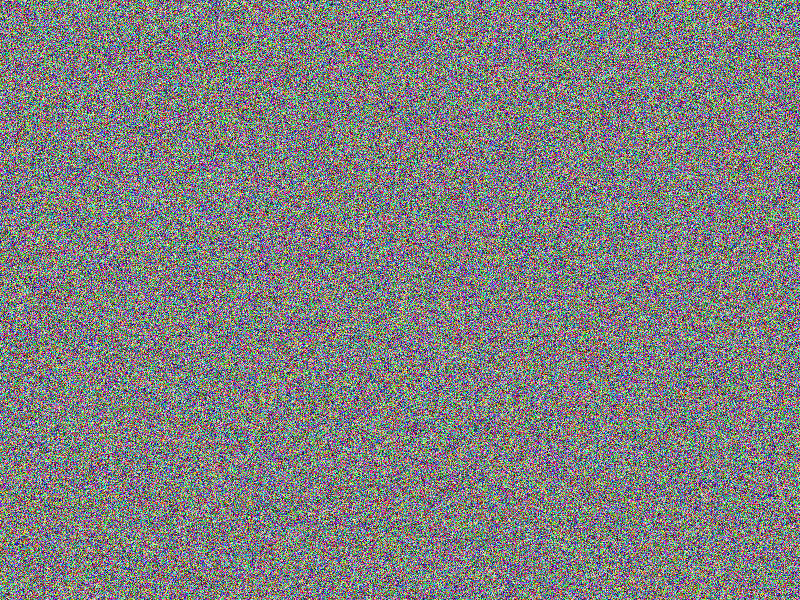A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
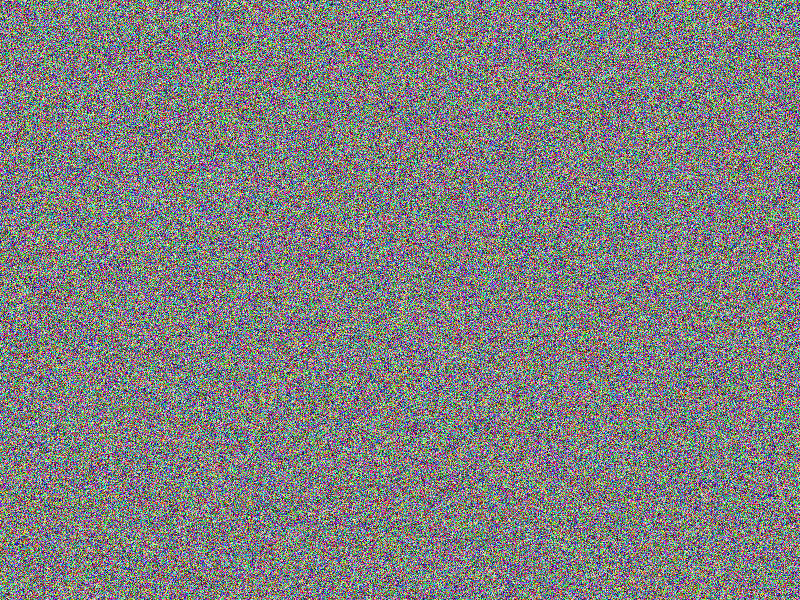A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS

CHAOS (NONE) encryption

Vanilla plain encryption does not reveal immediate correlation to the content of the original images (there seems already to be a quite good randomness), although the comparison of the encrypted images gives a first impression of the original images’ content (see the according bottom right images).

Facts

  • Algorithm: CHAOS-NONE
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 0
  • Entropy bits/byte (8 = best): 7.999869
  • Arithmetic mean (127.5 = random): 127.420840
  • Serial correlation (none = 0.0): -0.000196
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (XOR) encryption

Adding some XOR obfuscation during encryption does not lead to a convincing result. Comparing two very similar images not only reveal similar areas till the position where the images actually differ the fist time (notice the according bottom right image’s gray areas, indicating equal areas).

Facts

  • Algorithm: CHAOS-XOR
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 0
  • Entropy bits/byte (8 = best): 7.999878
  • Arithmetic mean (127.5 = random): 127.535873
  • Serial correlation (none = 0.0): 0.002190
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
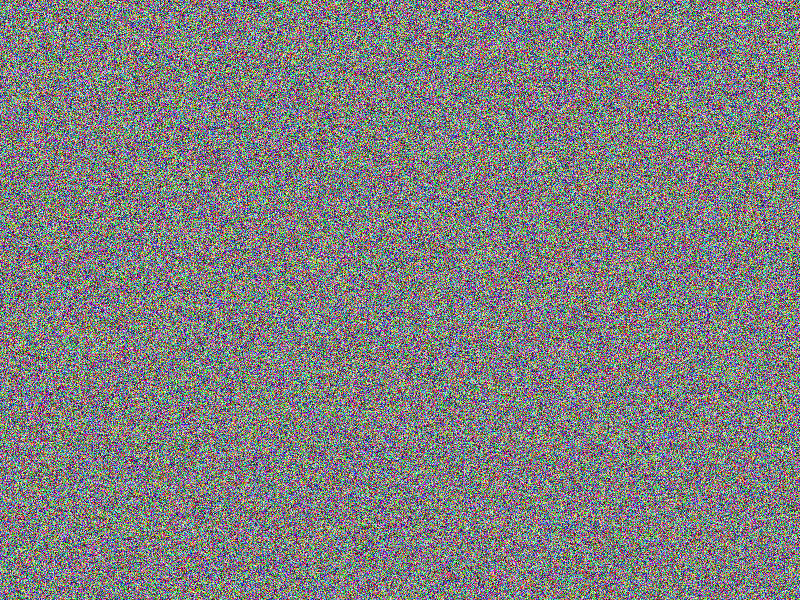A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
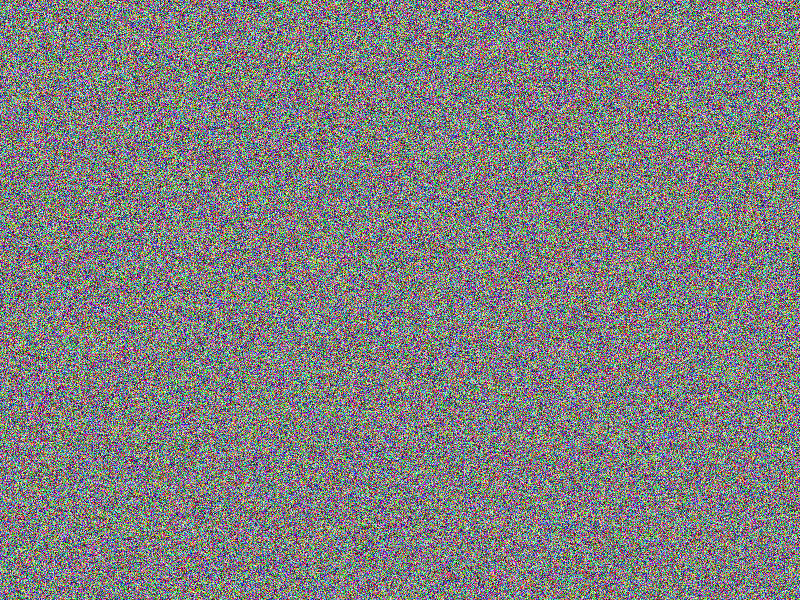A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (PREFIX32) encryption

Adding some PREFIX obfuscation during encryption does not lead to any improvement at all. The comparison of the encrypted images gives the same impression of the original images’ content as if no obfuscation at all would have been applied (see the according bottom right images). Actually, PREFIX obfuscation is not an obfuscation mode by itself, it only shows an effect when hardening the XOR and/or the MUTATE obfuscation!

Facts

  • Algorithm: CHAOS-PREFIX32
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 32
  • Entropy bits/byte (8 = best): 7.999855
  • Arithmetic mean (127.5 = random): 127.461611
  • Serial correlation (none = 0.0): -0.000197
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) 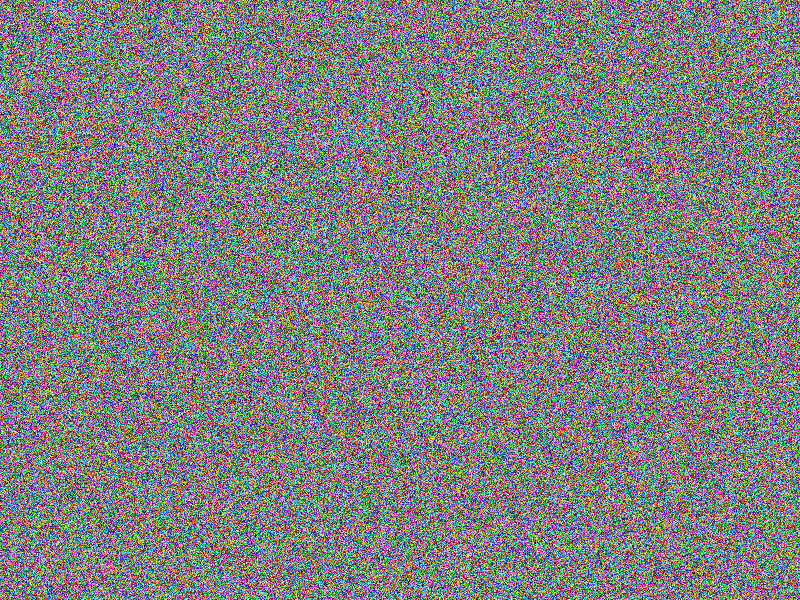Encrypted black and white squares
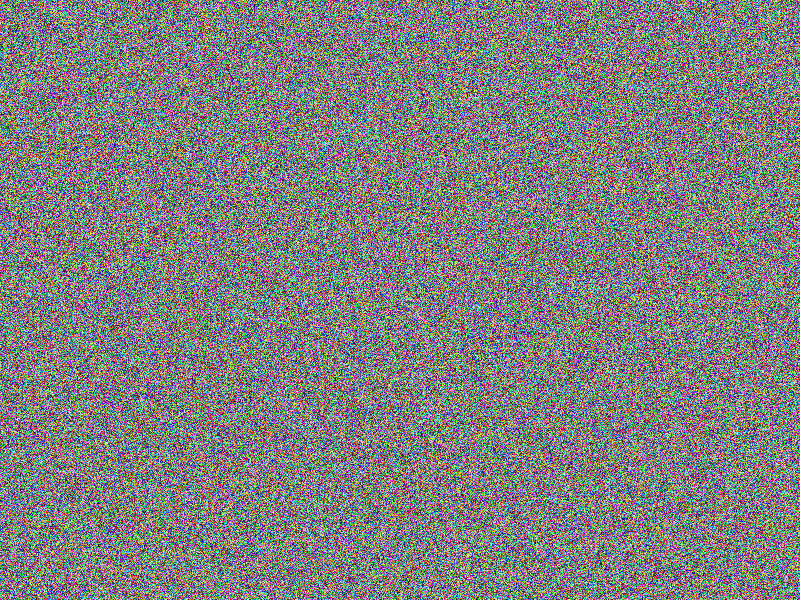A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
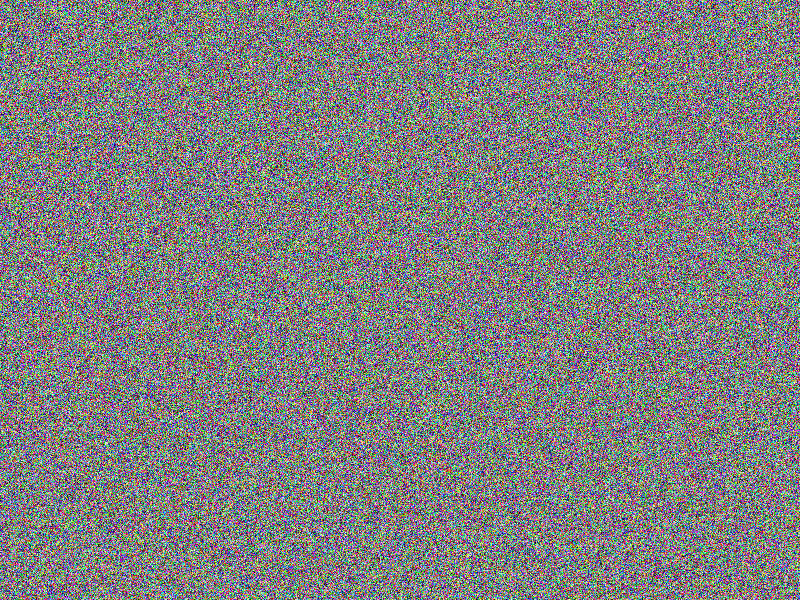Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
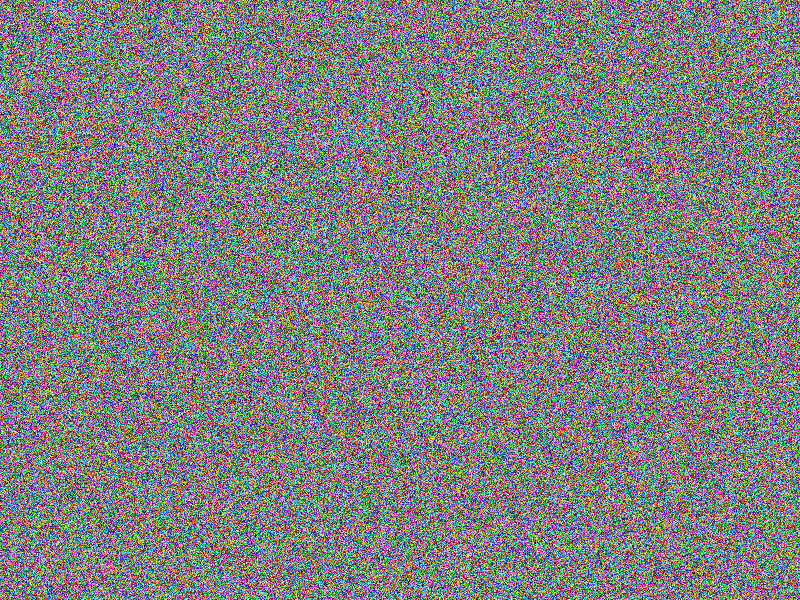B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) 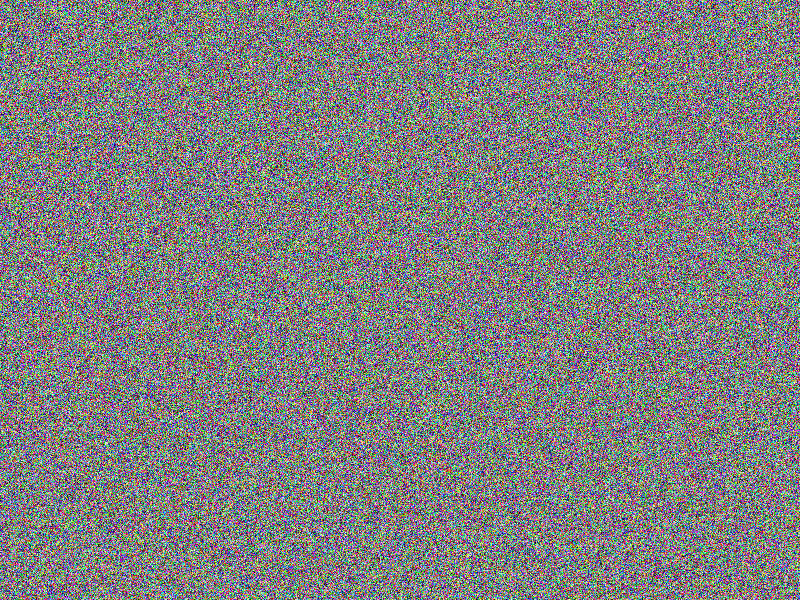Encrypted squares with circle
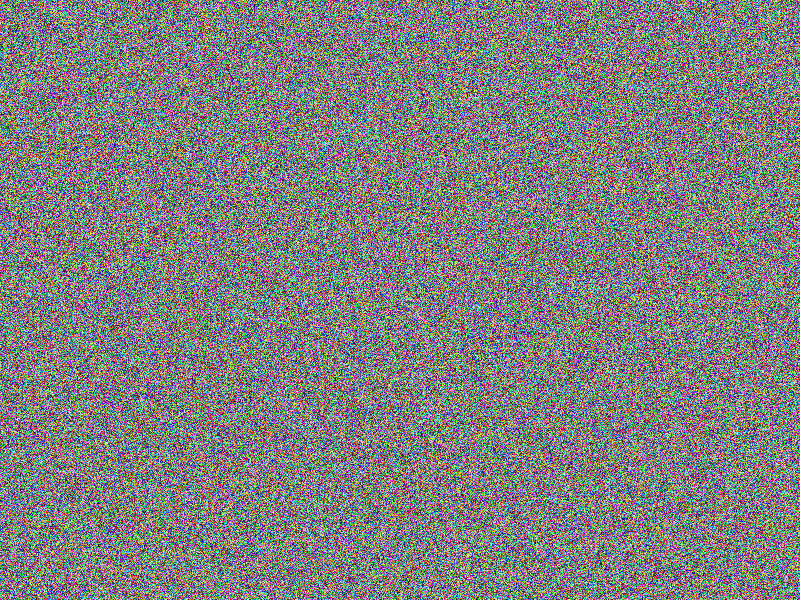A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (MUTATE) encryption

Adding some MUTATE obfuscation during encryption does not lead to a convincing result. Comparing two very similar images not only reveal similar areas till the position where the images actually differ the fist time (notice the according bottom right image’s gray areas, indicating equal areas).

Facts

  • Algorithm: CHAOS-MUTATE
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 0
  • Entropy bits/byte (8 = best): 7.999867
  • Arithmetic mean (127.5 = random): 127.506294
  • Serial correlation (none = 0.0): 0.000554
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
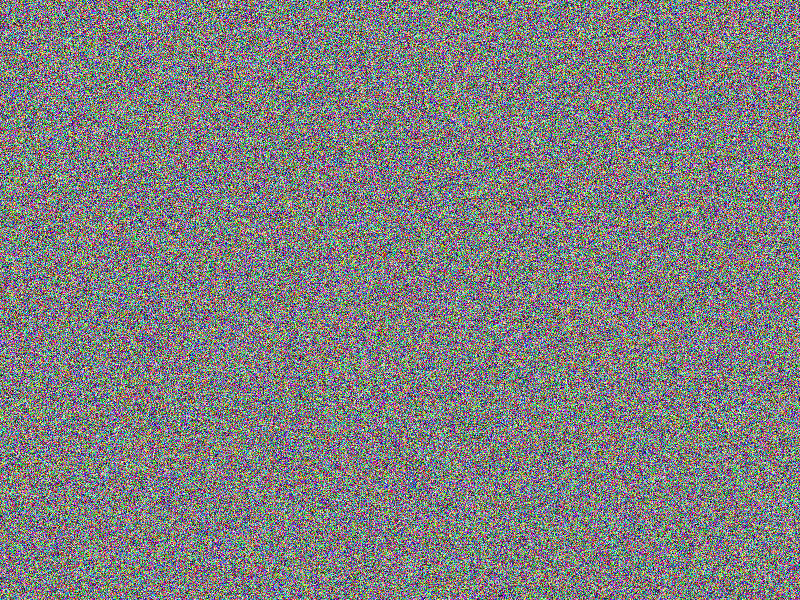A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
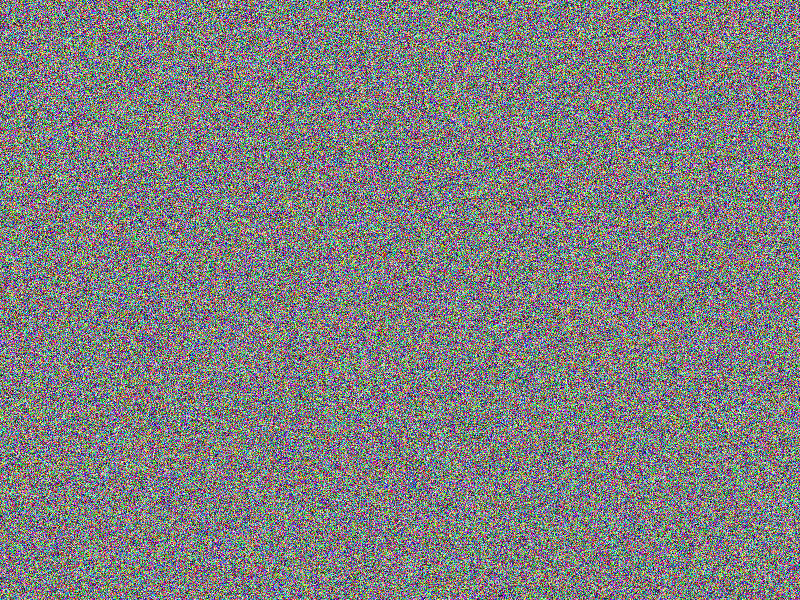A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (MUTATE-XOR) encryption

Combining MUTATE obfuscation with XOR mutation during encryption does not lead to a convincing result. Comparing two very similar images reveal similar areas till the position where the images actually differ the fist time (notice the according bottom right image’s gray areas, indicating equal areas).

Facts

  • Algorithm: CHAOS-MUTATE-XOR
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 0
  • Entropy bits/byte (8 = best): 7.999898
  • Arithmetic mean (127.5 = random): 127.500697
  • Serial correlation (none = 0.0): 0.000449
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) 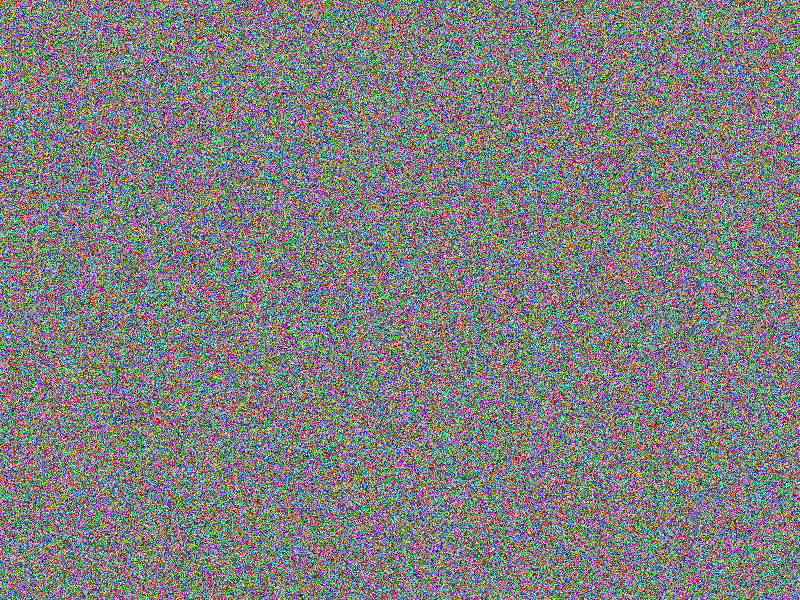Encrypted black and white squares
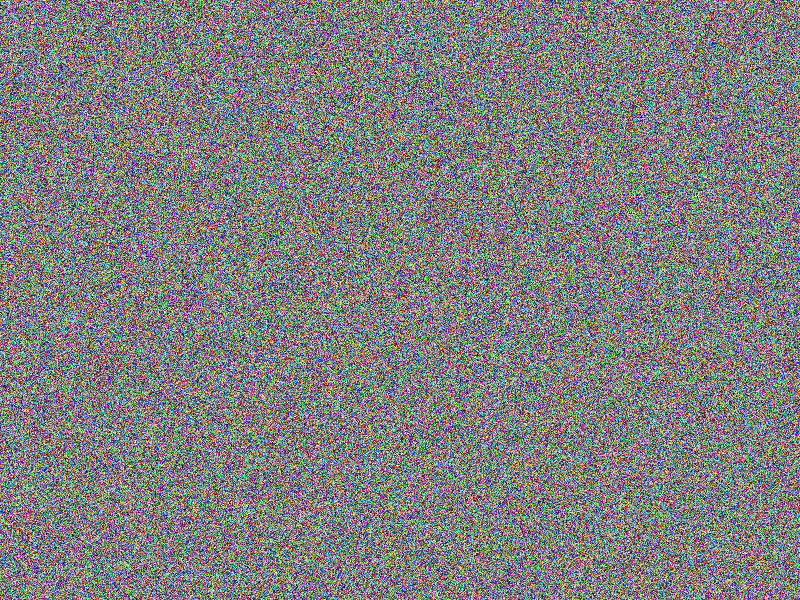A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
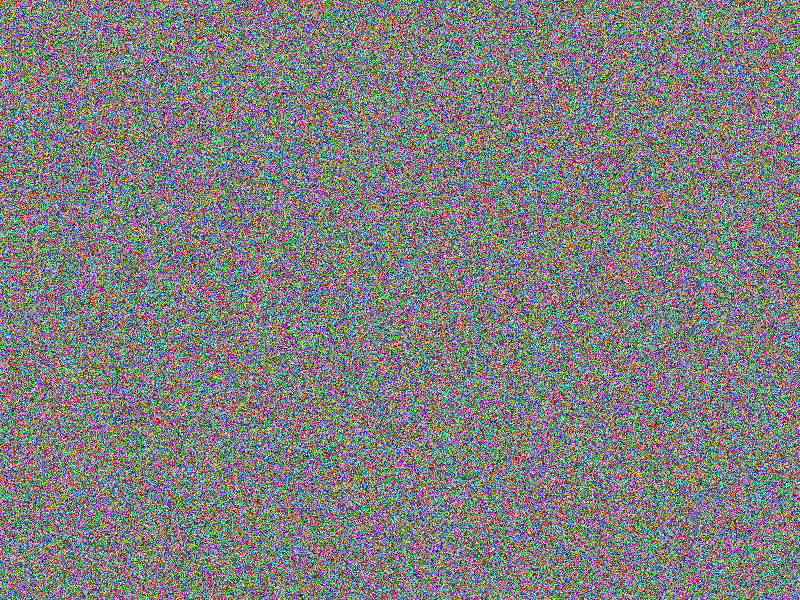B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
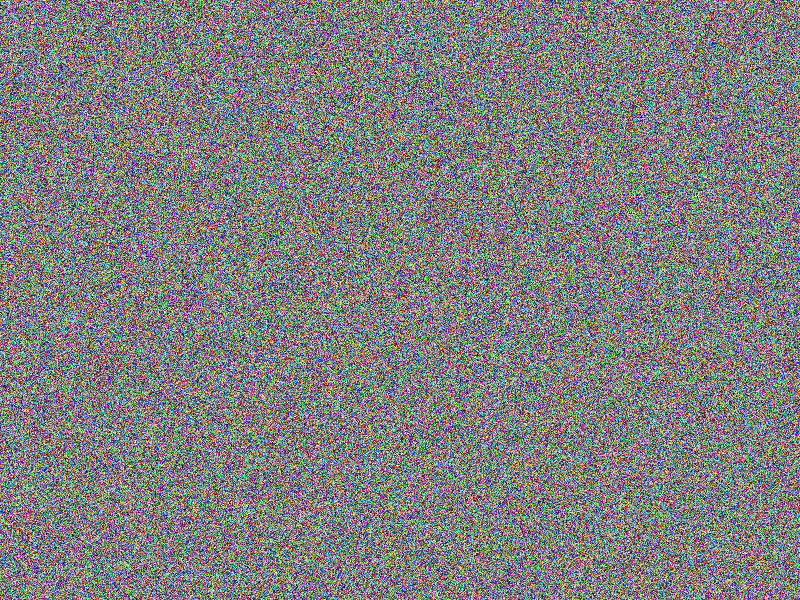A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (MUTATE-PREFIX32) encryption

Combining MUTATE obfuscation with PREFIX mutation during encryption does not lead to a convincing result. Comparing two very similar images still reveal few similar areas (notice the according bottom right image’s gray areas, indicating equal areas).

Facts

  • Algorithm: CHAOS-MUTATE-PREFIX32
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 32
  • Entropy bits/byte (8 = best): 7.999874
  • Arithmetic mean (127.5 = random): 127.545626
  • Serial correlation (none = 0.0): -0.001285
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) 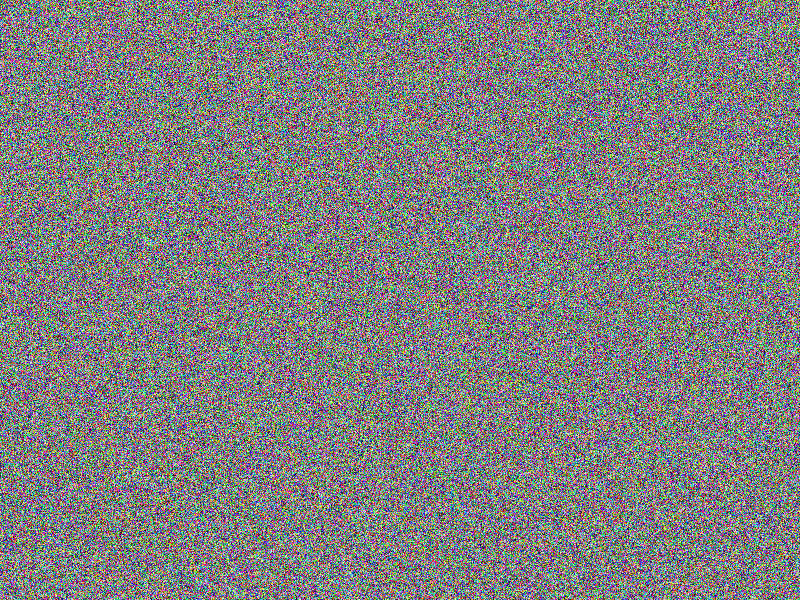Encrypted black and white squares
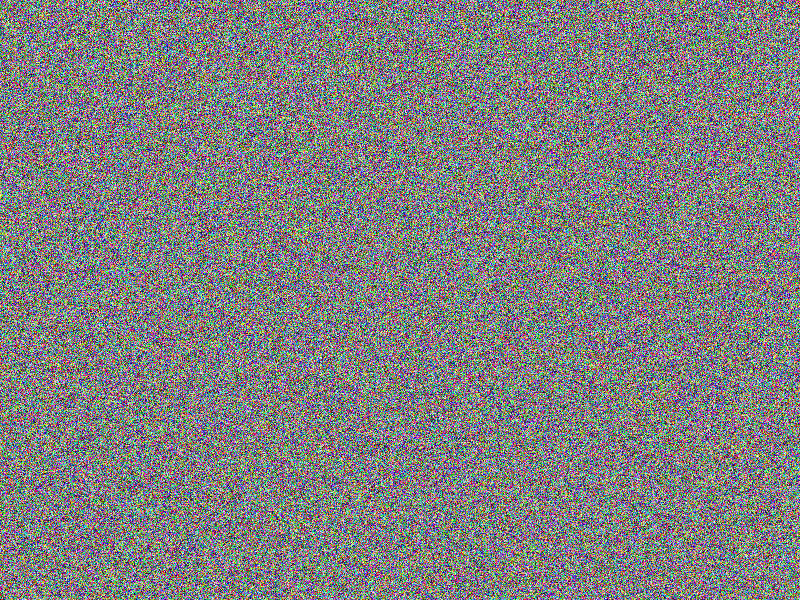A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
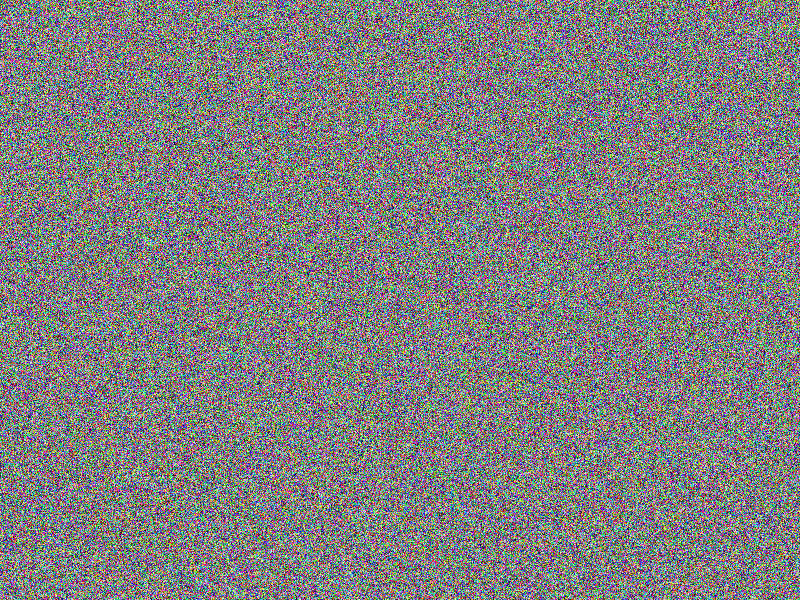B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
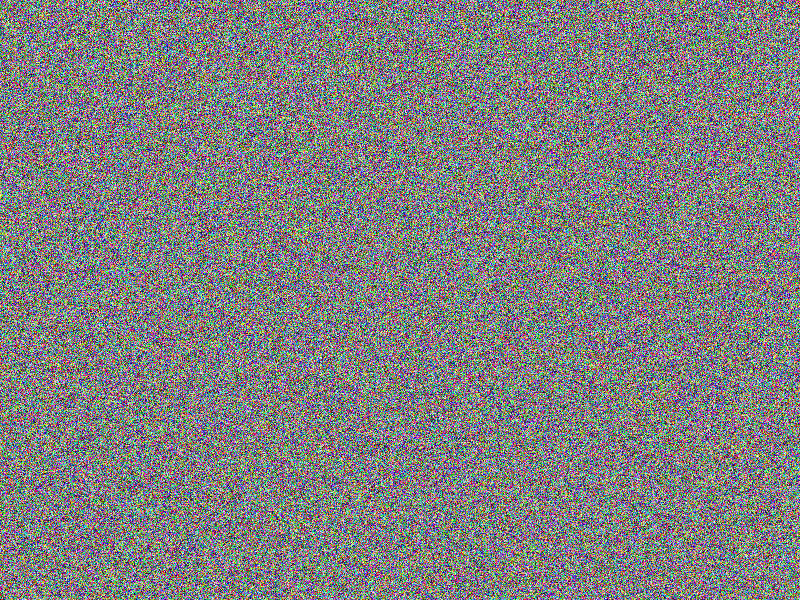A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (MUTATE-XOR-PREFIX32) encryption

The combination of all three MUTATE + XOR + PREFIX32 obfuscation variants makes comparing two very similar encrypted images hard (notice the according bottom right image being fully red, indicating no equal areas).

Facts

  • Algorithm: CHAOS-MUTATE-XOR-PREFIX32
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 32
  • Entropy bits/byte (8 = best): 7.999880
  • Arithmetic mean (127.5 = random): 127.527029
  • Serial correlation (none = 0.0): 0.000805
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
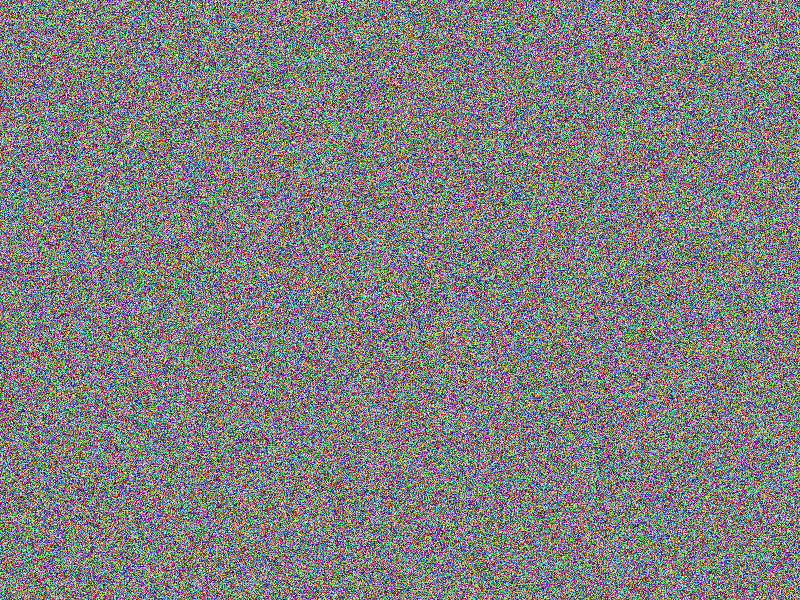A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
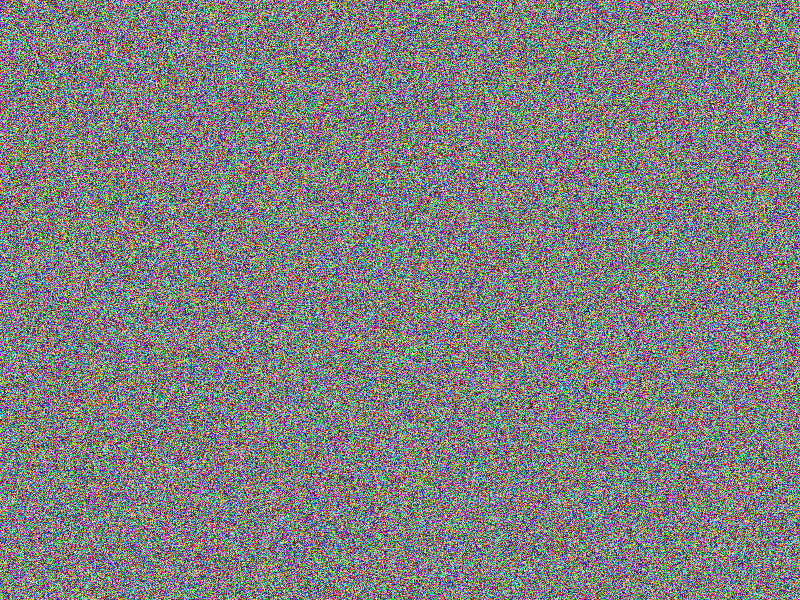Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) 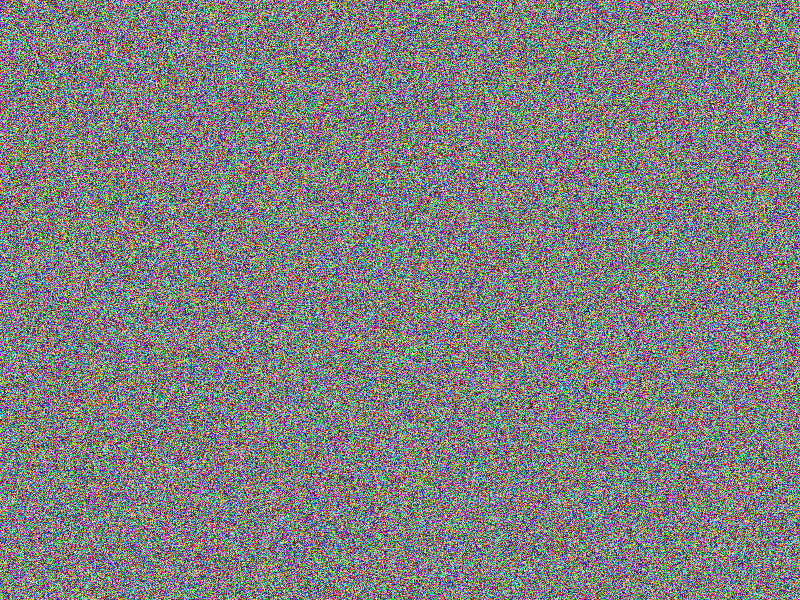Encrypted squares with circle
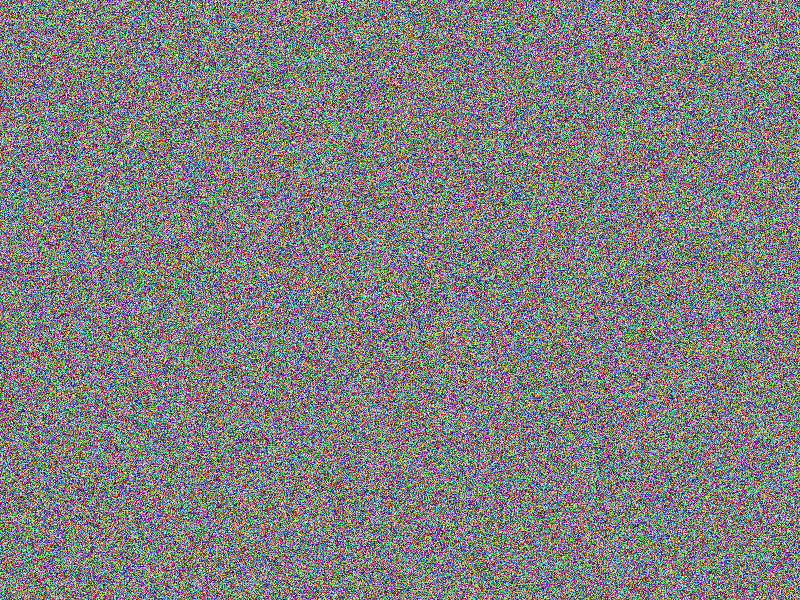A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (SALTED) encryption

Salted encryption looks perfect in that the comparison reveals no equal areas (notice the according bottom right image being fully red, indicating no equal areas) and the encrypted images look fully random.

Facts

  • Algorithm: CHAOS-SALTED
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 25
  • Entropy bits/byte (8 = best): 7.999869
  • Arithmetic mean (127.5 = random): 127.530544
  • Serial correlation (none = 0.0): 0.000776
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
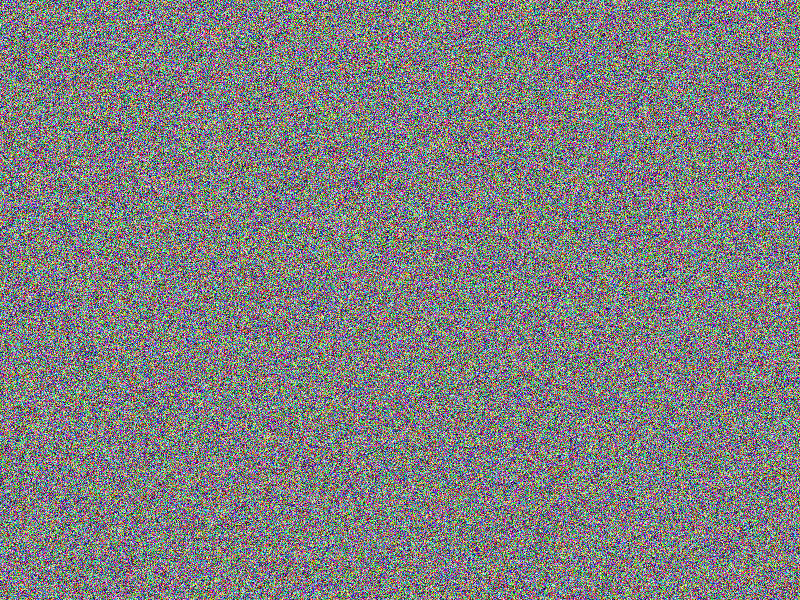A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
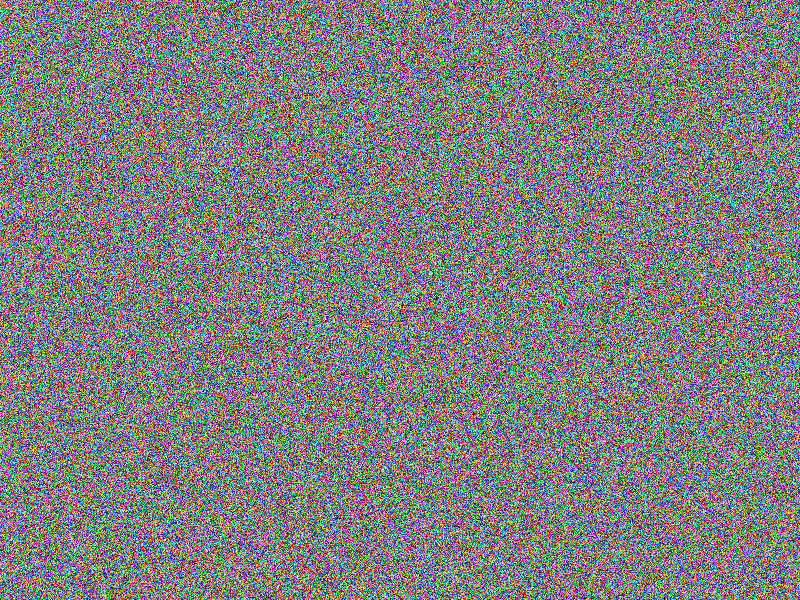Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
Encrypted   enc(A) ≏ enc(C) ~ (A,C) 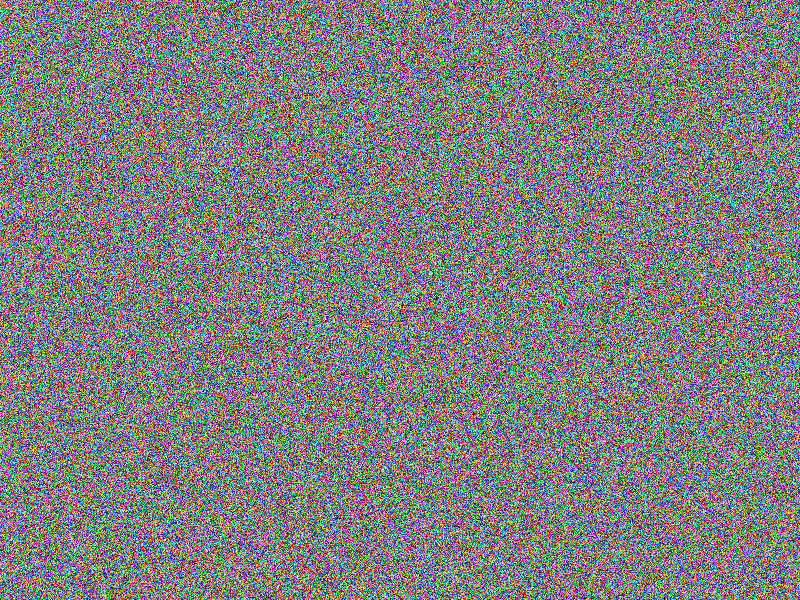Encrypted squares with circle
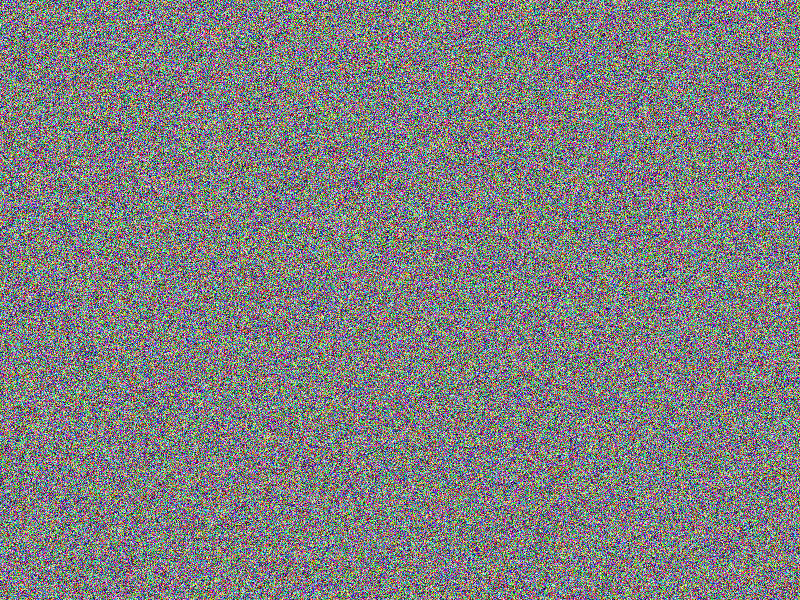A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

CHAOS (CERT) encryption

For scaling purposes, means are provided to apply an arbitrary number of encryption passes using a certificate of detailed instructions for each pass: Hence multiple passes with a mixture of obfuscation methods are applied, including XOR, PREFIX, MUTATE or SLATED obfuscations, alongside individual encryption keys, elongating the resulting “key” and hardening against brute force attacks.

Facts

  • Algorithm: CHAOS-CERT
  • Chain length: 8
  • First key: Salted = true, XOR = false, Mutate = false, Prefix = none
  • Second key: Salted = false, XOR = false, Mutate = true, Prefix = none
  • Other keys: Salted = false, XOR = false, Mutate = false, Prefix = none
  • Image file: A (blank image)
  • Image width: 800px
  • Image height: 600px
  • Algorithm prefix (bytes): 25
  • Entropy bits/byte (8 = best): 7.999887
  • Arithmetic mean (127.5 = random): 127.501808
  • Serial correlation (none = 0.0): -0.000777
  • Max compression (0% = none): 0%

A + B

  Original Encrypted B
Original     Black and white squares
Encrypted   enc(A) ≏ enc(B) ~ (A,B) Encrypted black and white squares
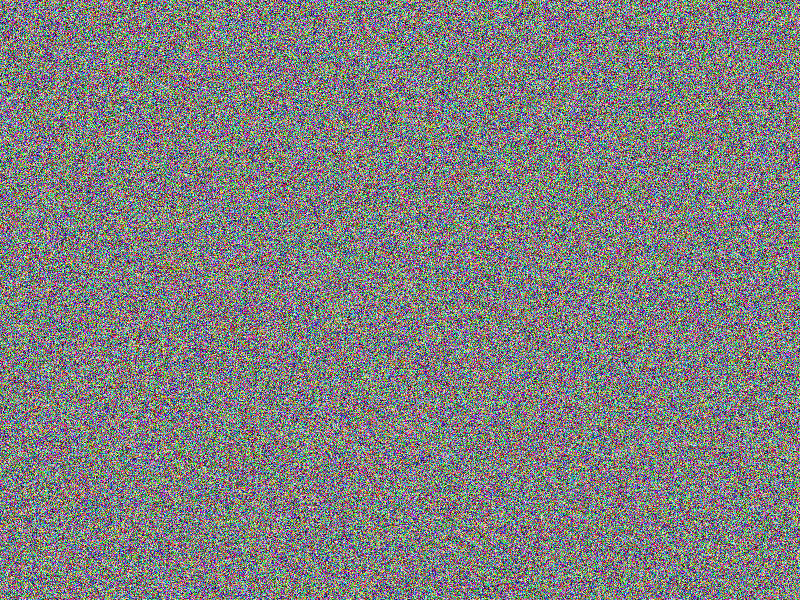A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

B + C

  Original Encrypted C
Original     Squares with circle
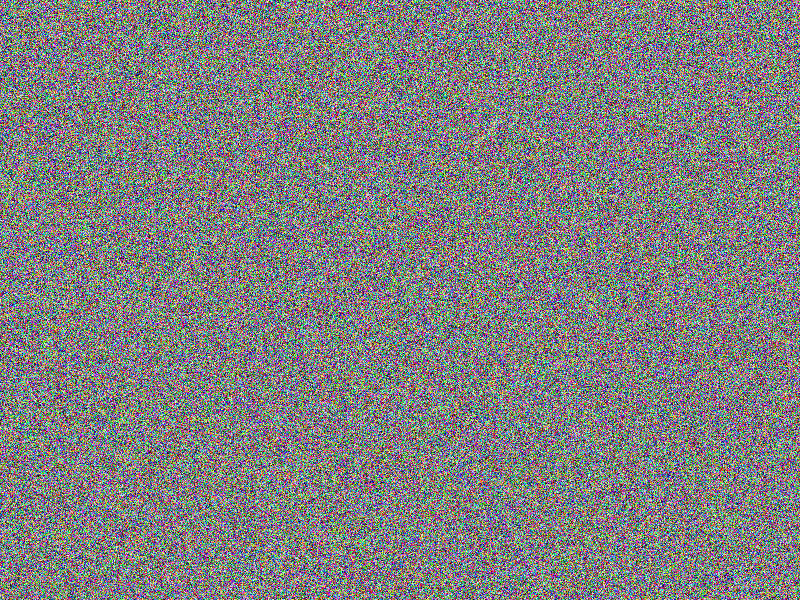Encrypted   enc(B) ≏ enc(C) ~ (B,C) Encrypted squares with circle
B Black and white squares Encrypted black and white squares Compare to encrypted black and white squares

A + C

  Original Encrypted C
Original     Squares with circle
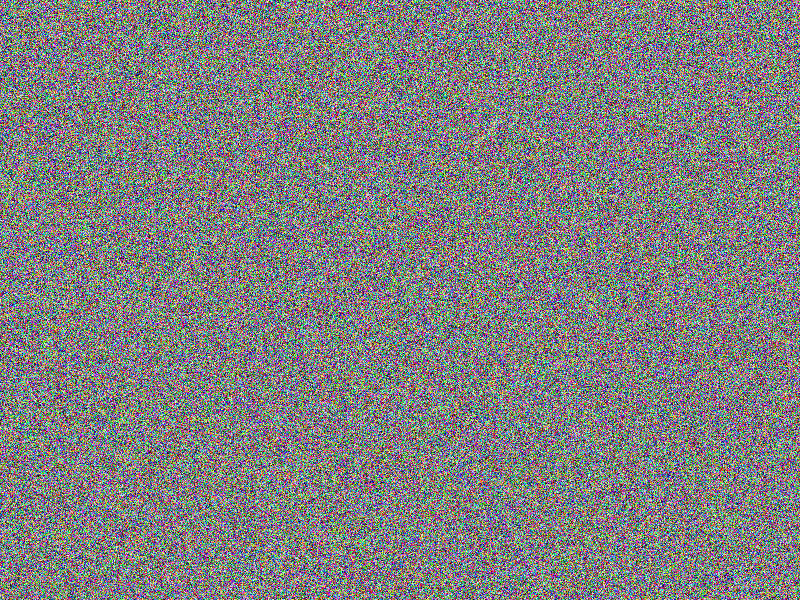Encrypted   enc(A) ≏ enc(C) ~ (A,C) Encrypted squares with circle
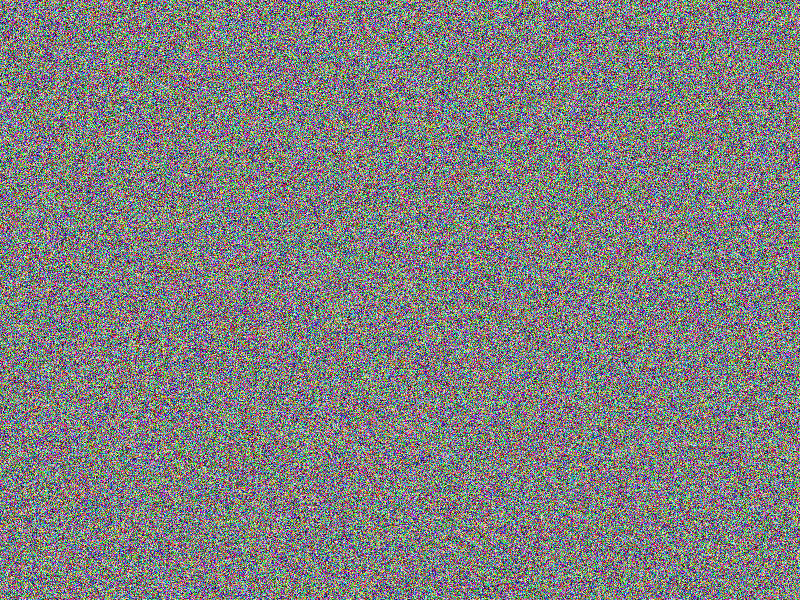A Blank canvas Encrypted blank canvas Compare to encrypted black and white squares

See also

  1. In the late 1980s Sönke Rehder provided me in Harare (Zimbabwe) with the pseudo code of the Chaos-based encryption algorithm ↩

  2. For a critical reflection, see Chaos-Based Cryptography: End of the Road? ↩

  3. See the downloads section of this site for other available variants of the tools ↩ ↩2

  4. Actually the salt is called “Initialization Vector” (IV) in the context of block ciphers, being the random per-encryption value ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7

  5. Estimated, please leave a message in case of correction ↩ ↩2 ↩3 ↩4

LinkedIn Reddit